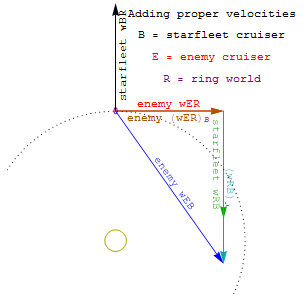
DescripcióSpaceBattle.png	English: A starfleet battle-cruiser drops out of hyperspace in the orbital plane of a ringworld, traveling at 1 ly/ty radially away from the ringworld's star. An enemy cruiser drops out of hyperspace nearby at the same time, traveling 1 ly/ty in the rotation-direction of the ringworld's orbit, and in a direction perpendicular to the starfleet cruiser's radial-trajectory . What is the proper-velocity (magnitude and direction) of the enemy cruiser relative to the starfleet ship?
Data	17 de febrer de 2014, 10:48:42
Font	Treball propi
Autor	P. Fraundorf
Altres versions	Aquesta imatge (de tipus physics) s'hauria de tornar a crear utilitzant gràfics vectorials com ara un fitxer SVG. Això té diversos avantatges; en trobareu més informació a Commons:Media for cleanup. Si ja disposeu d'una versió d'aquesta imatge en format SVG, us preguem que la pengeu; després, reemplaceu aquesta plantilla amb la plantilla {{Vector version available|nom nou de la imatge.svg}} en aquesta imatge.

As pointed out here^[1], local momenta per unit mass or proper-velocities w ≡ dx/dτ add as 3-vectors (in analogy to the classical expression v_AC = v_AB+v_BC), provided that we re-scale/direct the "out-of-frame" component w_AB and time-dilate w_BC according to:

${\displaystyle {\vec {w}}_{\text{AC}}={\vec {w}}_{A,B:C}+{\vec {w}}_{B:A,C}}$

where the first term is the non-proper "shared clock but not metric" velocity:

${\displaystyle {\vec {w}}_{A,B:C}={\vec {w}}_{AB\perp {\vec {w}}_{BC}}+\gamma _{\text{BC}}{\vec {w}}_{AB||{\vec {w}}_{BC}}}$

while the second term is the non-proper "shared metric but not clock" velocity:

${\displaystyle {\vec {w}}_{B:A,C}=\gamma _{\text{AB}}{\vec {w}}_{\text{BC}}}$.

One consequence of this is that w_CA (which uses A's rather than C's definition of simultaneity) will have the same magnitude as, but a different direction than, w_AC. Because the gamma factors are always greater than one, it is easy to see from the equation that the proper-velocity sum direction will be "Thomas-precessed" from w_AB+w_BC toward the direction of the intermediate frame's proper-velocity w_BC.

Note that we've now corrected the figure (and equations above) for a "Thomas-precession" rotation error in the solution above. A correction to the code listed below is also in the works. Unitsphere (discussió) 18:06, 20 July 2017 (UTC)

Coordinate-velocity 3-vectors do not similarly add. Also of course proper-velocity is proportional to momentum in the map-frame, while both proper-time (and proper-acceleration as needed in this context) are frame invariants.

This makes 3-vector velocities and accelerations much more useful at high-speeds in the traveler-kinematic^[2] (using proper-time τ, proper-velocity w ≡ dx/dτ and proper-acceleration α) than in the Galilean-kinematic^[3] (using map-time t, coordinate-velocity v ≡ dx/dt and coordinate-acceleration a ≡ dv/dt).

Aside: Note that the orbiting ringworld depicted above is more like those in Bungie corporation's Halo universe, than the immense concentric structure described in Larry Niven's ringworld universe.

A challenging follow-on to this might be to ask how long it would take to catch up to and dock with the enemy, assuming that its speed and direction are fixed, while your ship is capable of 1-gee acceleration. Any volunteers?

Some useful Mathematica 8.0 declarations for use with two or three-vector arguments, regardless of the speeds and directions involved, include:

gammaw[w_] := Sqrt[1 + w.w]

wABbyCn[wAB_, wBC_] := wAB + (gammaw[wBC] - 1) wAB.wBC/wBC.wBC wBC

wBCbyCn[wAB_, wBC_] := gammaw[wAB] wBC

wACbyCn[wAB_, wBC_] := wABbyCn[wAB, wBC] + wBCbyCn[wAB, wBC]

Here we set up the problem by specifying (in lightspeed units) the proper-velocity vectors of the starfleet battle-cruiser B with respect to the ring (R), and of the enemy battle-cruiser (E) with respect to the ring. Finally, we specify the xy coordinates of the ring relative to its own star in the diagram:

wBR = {0, 1}; wER = {1, 0}; halo = {0, 1.2};

Answers:

enemyProperSpeedEB = Norm[wACbyCn[wER, -wBR]]

This yields wEB = Sqrt[3] in units of ly/ty.

enemyDirectionEB = 
ArcTan[wACbyCn[wER, -wBR]1, wACbyCn[wER, -wBR]2]*180./Pi

This puts the angle at -54.7356 degrees.

The plot is might be made by the following command:

Graphics[
 {
  Darker[Yellow], Circle[{0, 0}, .1],
  Purple, Circle[halo, {.015, .03}],
  Black,
  Arrow[{halo, halo + wBR}],
  Text["bship wBR", halo + wBR/2, {0, -1}, -wBR],
  Red,
  Text["enemy wER", halo + wER/2, {0, -1}, wER],
  Arrow[{halo, halo + wER}],
  Blue,
  Arrow[{halo, halo + wACbyCn[wER, -wBR]}],
  Text["enemy wEB", 
   halo + wACbyCn[wER, -wBR]/2, {0, -1}, {wACbyCn[wER, -wBR][[1]], 
    wACbyCn[wER, -wBR][[2]]}],
  Darker[Green],
  Arrow[{halo(*+wABbyCn[wER,-wBR]*), 
    halo(*+wABbyCn[wER,-wBR]*)- wBR}], 
  Text["ring wRB", halo(*+wABbyCn[wER,-wBR]*)- wBR/2, {0, 1}, -wBR],
  Gray,
  Dashed, 
  Line[{halo, halo + wABwithBtoC, halo + wAC, halo + wBCwithBtoA, 
    halo}],
  Darker[Cyan],
  Arrow[{halo + wABbyCn[wER, -wBR], 
    halo + wBCbyCn[wER, -wBR] + wABbyCn[wER, -wBR]}],
  Text["ring (wRB)R\[Rule]E", 
   halo + wABbyCn[wER, -wBR] + wBCbyCn[wER, -wBR]/2, {0, -1}, 
   wBCbyCn[wER, -wBR]],
  Darker[Orange],
  Arrow[{halo, halo + wABbyCn[wER, -wBR]}],
  Text["enemy (wER)R\[Rule]B", halo + wABbyCn[wER, -wBR]/2, {0, 1}, 
   wABbyCn[wER, -wBR]],
  Black, Dotted,
  Circle[{0, 0}, Norm[halo]],
  Text["Find wEB from wER and wRB", labelHigh(*{.9,3.0}*)],
  Text["B = starfleet battleship", labelHigh - {0, 0.2}],
  Red, Text["E = enemy cruiser", labelHigh - {0, 0.4}],
  Purple, Text["R = ring world", labelHigh - {0, 0.6}]
  },
 PlotRange -> pRange(*{{-1,2},{-.5,2.5}}*),
 BaseStyle -> {FontFamily -> "Courier", FontSize -> 12}
 ]

1. ↑ P. Fraundorf (2016/2017) Traveler-point dynamics, hal-01503971 working draft on-line discussion^{[dead link]}.
2. ↑ P. Fraundorf (2012) "A traveler-centered intro to kinematics", arxiv:1206.2877 [physics.pop-ph].
3. ↑ Anthony P. French (1968) Special relativity (W. W. Norton, NY) page 154: "...acceleration is a quantity of limited and questionable value in special relativity."

Jo, el titular dels drets d'autor d'aquest treball, el public sota la següent llicència:

Aquest fitxer està subjecte a la llicència Creative Commons Reconeixement-CompartirIgual 3.0 No adaptada.

Sou lliure de:

• compartir – copiar, distribuir i comunicar públicament l'obra
• adaptar – fer-ne obres derivades

Amb les condicions següents:

• reconeixement – Heu de donar la informació adequada sobre l'autor, proporcionar un enllaç a la llicència i indicar si s'han realitzat canvis. Podeu fer-ho amb qualsevol mitjà raonable, però de cap manera no suggereixi que l'autor us dóna suport o aprova l'ús que en feu.
• compartir igual – Si modifiqueu, transformeu, o creeu a partir del material, heu de distribuir les vostres contribucions sota una llicència similar o una de compatible amb l'original.

https://creativecommons.org/licenses/by-sa/3.0CC BY-SA 3.0 Creative Commons Attribution-Share Alike 3.0 truetrue