Pèndol

Trajectòria d'un pèndol simple amb la descomposició de forces

Un pèndol és un sistema físic construït per un sòlid sotmès a l'acció de la gravetat i subjectat de manera que pot girar lliurement sobre un eix que no passa pel seu centre de gravetat. Un model simplificat del pèndol, útil per establir-ne les lleis generals, és el pèndol simple o pèndol matemàtic, format per una un fil flexible, inextensible i de massa negligible, agafat per un extrem superior d'un punt fix, amb una massa puntual en el seu extrem inferior que oscil·la lliurement en el buit. Si el moviment de la massa es manté en un pla, es diu que és un pèndol pla; en cas contrari, es diu que és un pèndol esfèric.

El principi del pèndol fou descobert per l'astrònom i físic italià Galileu, que va establir que, per amplituds petites, el període d'oscil·lació és independent de l'amplitud (distància màxima que s'allunya el pèndol de la posició d'equilibri).

Algunes aplicacions del pèndol són la mesura del temps, el metrònom i la plomada. Una altra aplicació es coneix com el Pèndol de Foucault, el qual s'empra per evidenciar la rotació de la Terra. Es diu així en honor del físic francès León Foucault i està format per una gran massa suspesa d'un cable molt lleuger.

Història

Rèplica del sismòmetre de Zhang Heng. El pèndol està contingut al seu interior.

Un dels primers usos coneguts d'un pèndol va ser un dispositiu de sismòmetre del Plantilla:Segle de la dinastia Han científic xinès Zhang Heng. Era concebut per a balancejar-se i activar una d'una sèrie de palanques després de ser pertorbada pel tremolor d'un terratrèmol llunyà. Alliberada per una palanca, una petita bola queia del dispositiu en forma d'urna en una de les vuit boques de gripau de metall que hi havia a sota, als vuit punts de la brúixola, significant la direcció en què es trobava el terratrèmol.

Moltes fonts afirmen que l'astrònom egipci del Plantilla:Segle Ibn Yunus utilitzava un pèndol per mesurar el temps, però es tracta d'un error originat el 1684 per l'historiador britànic Edward Bernard.

Durant el Renaixement, s'utilitzaven grans pèndols bombats a mà com a fonts d'energia per a màquines manuals de moviment alternatiu, com serres, manxes i bombes. Leonardo da Vinci va fer molts dibuixos del moviment dels pèndols, encara que sense adonar-se del seu valor per al mesurament del temps.

1602: Investigacions de Galileo

El científic italià Galileo Galilei (1564-1642) va ser el primer a estudiar les propietats dels pèndols, al voltant de 1602. El primer informe que es conserva de les seves investigacions està contingut en una carta a Guido Ubaldo dal Monte, des de Pàdua, datada el 29 de novembre de 1602. El seu biògraf i estudiant, Vincenzo Viviani, indica que el seu interès s'havia despertat cap a 1582 pel moviment oscil·latori d'un canelobre de la catedral de Pisa. Galileu va descobrir que la propietat important que fa al pèndol una eina útil per mesurar el temps, anomenada isocronisme; el període del pèndol és aproximadament independent de l'amplitud o el desplaçament del balanceig. També va descobrir que el període és independent de la massa de la llentia i proporcional a l'arrel quadrada de la longitud del pèndol. Primer va emprar pèndols de lliure oscil·lació en aplicacions simples de temporització. El seu amic mèdic, Santorio Santorii, va inventar un dispositiu que mesurava el pols d'un pacient per la longitud d'un pèndol; el pulsilogium. En 1641 Galileu li va dictar al seu fill Vincenzo el disseny d'un rellotge de pèndol; Vincenzo va començar a construir-lo, però no l'havia acabat quan va morir el 1649.

1656: El rellotge de pèndol

Plantilla:Imatge múltiple En 1656 el científic neerlandès Christiaan Huygens va construir el primer rellotge de pèndol. Això va suposar una gran millora respecte als rellotges mecànics existents; la precisió va passar d'uns 15 minuts de desviació al dia a uns 15 segons al dia. Els pèndols es van estendre per Europa a mesura que els van integrar en els rellotges existents.

El científic anglès Robert Hooke va estudiar el pèndol cònic cap a 1666, consistent en un pèndol que es balanceja lliurement en dues dimensions, amb la bobina girant en un cercle o el·lipse. Va utilitzar els moviments d'aquest aparell com a model per analitzar els moviments orbitals dels planetes. Hooke va suggerir a Isaac Newton el 1679 que els components del moviment orbital consistien en un moviment inercial al llarg d'una direcció tangent més un moviment atractiu en la direcció radial. Això va jugar un paper en la formulació de Newton de la llei de la gravitació universal. Robert Hooke també va ser el responsable de suggerir ja el 1666 que el pèndol podia servir per a mesurar la força de la gravetat.

Durant una expedició a Caiena a la Guaiana Francesa el 1671, Jean Richer va descobrir que un rellotge de pèndol era Plantilla:Frac minuts per dia més lent a Caiena que a París. D'això va deduir que la força de la gravetat era menor a Caiena.

Pèndol simple o matemàtic

Components del pes de la massa pendular.

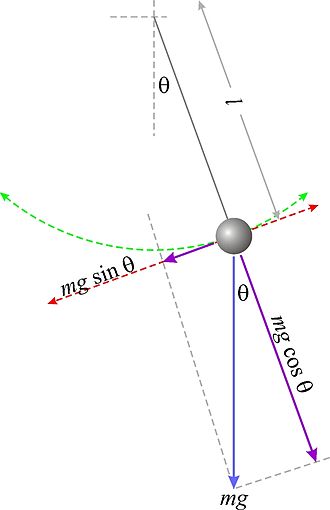
També anomenat pèndol ideal, està constituït per un fil inextensible de massa negligible, sostingut pel seu extrem superior d'un punt fix, amb una massa puntual subjecta al seu extrem inferior que oscil·la lliurement en un pla vertical fix.

En separar la massa pendular del seu punt d'equilibri, oscil·la a banda i banda d'aquesta posició, desplaçant-se sobre una trajectòria circular amb moviment diari.

Equació del moviment

Per escriure l'equació del moviment observarem la figura adjunta corresponent a una posició genèrica del pèndol. La fletxa blava representa el pes de la massa pendular. Les fletxes en color violeta representen les components del pes a les direccions tangencial i normal a la trajectòria.

Aplicant la Segona llei de Newton a la direcció del moviment, tenim Plantilla:Equació on el signe negatiu té en compte que la $F_{\text{t}}$ té direcció oposada a la del desplaçament angular positiu (cap a la dreta, a la figura). Considerant la relació existent entre l'acceleració tangencial i l'acceleració angular Plantilla:Equació obtenim finalment l'equació diferencial del moviment pla del pèndol simple Plantilla:Equació

Període d'oscil·lació

Factor damplificació del període dun pèndol, per a una amplitud angular qualsevol. Per a angles petits el factor val aproximadament 1, però tendeix a infinit per a angles propers a π (180°).

L'astrònom i físic italià Galileo Galilei va observar que el període d'oscil·lació és independent de l'amplitud, almenys per a petites oscil·lacions. Per contra, aquell depèn de la longitud del fil. El període de l'oscil·lació d'un pèndol simple restringit a oscil·lacions de petita amplitud es pot aproximar per: Plantilla:Equació Per a oscil·lacions majors la relació exacta per al període no és constant amb l'amplitud i involucra integrals el·líptiques de primera espècie:

$T=4\sqrt{\frac{\ell }{g}}K(\mathrm{sen}\frac{{\phi }_0}{2})=4\sqrt{\frac{\ell }{g}}\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{d\theta }{\sqrt{1-{\mathrm{sen}}^2\frac{{\phi }_0}{2}{\mathrm{sen}}^2\theta }}$

On φ₀ és l'amplitud angular màxima. L'equació anterior es pot desenvolupar a la sèrie de Taylor obtenint-se una expressió més útil:

$T=2\pi \sqrt{\frac{\ell }{g}}[1+{\left(\frac{1}{2}\right)}^2{\mathrm{sen}}^2\frac{{\phi }_0}{2}+{\left(\frac{1\cdot 3}{2\cdot 4}\right)}^2{\mathrm{sen}}^4\frac{{\phi }_0}{2}+{\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)}^2{\mathrm{sen}}^6\frac{{\phi }_0}{2}+\dots ]$

Solució de l'equació de moviment

Per a petites oscil·lacions, l'amplitud és gairebé sinusoïdal, per amplituds més grans l'oscil·lació ja no és sinusoïdal. La figura mostra un moviment de gran amplitud ${\varphi }_0=0,999\pi$ (negre), juntament amb un moviment de petita amplitud ${\varphi }_0=0,25\pi$ (gris).

Per a amplituds petites, l'oscil·lació es pot aproximar com a combinació lineal de funcions trigonomètriques. Per amplituds grans pot provar-se l'angle pot expressar-se com a combinació lineal de funcions el·líptiques de Jacobi. Per veure això només cal tenir en compte que l'energia constitueix una integral de moviment i utilitzar el mètode de la quadratura per integrar l'equació de moviment: Plantilla:Equació On, en la darrera expressió s'ha fet servir la fórmula de l'angle doble i on a més:

$E=-mgl\cos {\varphi }_0$, és l'energia, que està relacionada amb la màxima amplitud ${\varphi }_0$.

$U(\varphi )=-mgl\cos \varphi$, és l'energia potencial.

Realitzant en variable $\mathrm{sen}\xi =\frac{\mathrm{sen}\frac{\theta }{2}}{\mathrm{sen}\frac{{\varphi }_0}{2}}$, la solució de les equacions del moviment es pot expressar com:

On:

$\text{sn}(t)$, és la funció el·líptica de Jacobi de tipus sinus.

$\mathrm{sen}\mathrm{\Phi }=\frac{\mathrm{sen}\frac{\varphi (t)}{2}}{\mathrm{sen}\frac{{\varphi }_0}{2}}$

El lagrangià del sistema és $ℒ=T-V=\frac{1}{2}m{l}^2{\dot{\theta }}^2+mgl\cos \theta$, on $\theta$ és l'angle que forma la corda del pèndol al llarg de les oscil·lacions (és la variable), i $l$ és la longitud de la corda (és la lligadura). Si s'apliquen les equacions de Lagrange s'arriba a l'equació final del moviment: $l^2\ddot{\theta }+gl\mathrm{sen}\theta =0$. És a dir, la massa no influeix en el moviment d'un pèndol.

Vegeu també

• Oscil·lador harmònic
• Doble pèndol
• Metrònom
• Pèndol balístic
• Pèndol cicloïdal
• Pèndol cònic
• Pèndol de Foucault
• Pèndol de Kater
• Pèndol de Newton
• Pèndol de Pohl
• Pèndol de torsió
• Pèndol esfèric
• Pèndol simple
• Pèndol simple equivalent
• Rellotge de pèndol
• Teorema de Huygens