Trajectòria balística

La trajectòria balística és la trajectòria de vol que segueix un projectil sotmès únicament a la seva pròpia inèrcia i a les forces inherents al medi en el qual es desplaça, principalment la força gravitatòria. La ciència que estudia els fenòmens balístics en general es denomina balística. Quan sobre el projectil tan sols actua la gravetat, la trajectòria balística és una paràbola, però la presència d'altres forces, com ara la resistència aerodinàmica de l'atmosfera, la força de sustentació, l'efecte Coriolis de la rotació terrestre, etc. fan que la trajectòria real sigui quelcom diferent d'una paràbola.

Míssils balístics

Alguns projectils autopropulsats s'anomenen balístics atès que no hi ha propulsió res més que en la fase inicial de propulsió, un exemple d'això són els míssils balístics que en la seva fase de caiguda no tenen autopropulsió.

Equacions de la trajectòria balística

Figura 1. Esquema de la trajectòria del moviment balístic.

Objecte disparat amb un angle inicial ${\theta }_0$ des d'un punt $y(x_0)$ que segueix una trajectòria parabòlica .

Utilitzarem les següents hipòtesis simplificadores:

• L'abast del projectil és suficientment petit com per poder menysprear la curvatura de la superfície terrestre (l'acceleració gravitatòria $𝐠$ és normal a aquesta superfície);
• L'altura que aconsegueix el projectil és suficientment petita com per poder menysprear la variació del camp gravitatori terrestre amb l'altura;
• La velocitat del projectil és suficientment petita com per poder menysprear la resistència que presenta l'aire al seu moviment;
• No tindrem en compte l'efecte de rotació de la Terra que, com veurem més endavant, tendeix a desviar el projectil cap a la dreta de la seva trajectòria quan el moviment té lloc en l'hemisferi Nord.

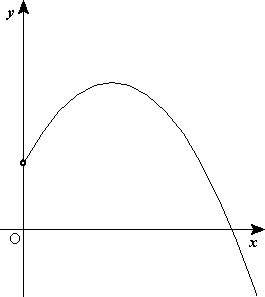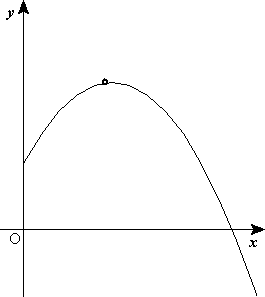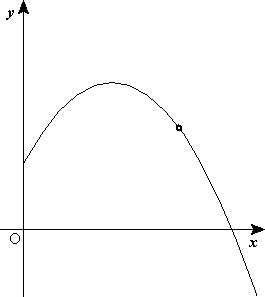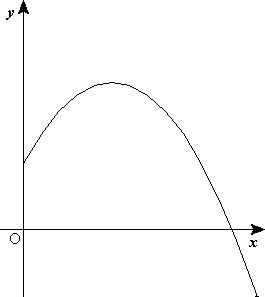
Suposem que es dispara el projectil amb una velocitat inicial ${𝐯}_0$ que forma un angle ${\mathit{\theta }}_0$ amb l'horitzontal. Escollirem el pla xy coincidint amb el pla de la trajectòria (definit per ${𝐯}_0$ y $𝐠$), amb l'eix y vertical i dirigit cap amunt i l'origen O coincidint amb la posició de tir del projectil. Tenim:

La component horitzontal de la velocitat roman invariable, però la component vertical canvia en el transcurs del temps. A la figura 1 s'observa que el vector velocitat inicial $v_0$ forma un angle inicial ${\theta }_0$ respecte a l'eix x ; l'angle <$\theta$ que forma la velocitat amb l'horitzontal, que coincideix amb el pendent de la trajectòria, canvia conforme avança el projectil.

Integrant les ec. (3) i tenint en compte les condicions inicials (2)

Mitjançant nova integració de (4), amb les condicions inicials (1), obtenim el vector de posició del projectil:

Aquestes dues equacions constitueixen les equacions paramètriques de la trajectòria. Si eliminem el temps entre les expressions de les components xiy del vector de posició amb les equacions que donen les posicions $x$ y $y$, obtindrem l'equació algebraica de la trajectòria, això és:

que representa una paràbola en el plànol x, y .

A la figura 1 es mostra aquesta representació, però en ella s'ha considerat $y_0=0$ (però no en l'animació respectiva). En aquesta figura també s'observa que l'altura màxima en la trajectòria parabòlica es produirà en H, quan la component vertical de la velocitat $v_y$ sigui nul·la (màxim de la paràbola), i que l'abast horitzontal $x$ passarà quan el cos retorni a terra, en $y=0$ (on la paràbola talla l'eix $x$).

A partir de les equacions anteriors podem obtenir molta informació sobre el moviment del projectil.

Per exemple, en el cas que $y_0=0$, el temps $t_h$ necessari perquè el projectil arribi a l'altura màxima $h$ el determinem anul·lant la component vertical de la velocitat en [4], ja que en aquest punt la velocitat del projectil és horitzontal. L'altura màxima $h$ aconseguida pel projectil i el recorregut horitzontal $x_h$ realitzat fins a aquest instant els calculem substituint el temps $t_h$ en les components del vector de posició $𝐫$ en [5], obtenint:

El temps $t_A$ que empra el projectil a retornar al pla horitzontal de llançament rep el nom de temps de vol i ho podem calcular fent $y=0$ en [5]. El abast $x_A$ és la distància horitzontal coberta durant aquest temps i es determina substituint el valor del temps de vol en $x(t)$ en [5]:

Observeu que $t_A=2t_h$, que $x_A=2x_h$ i que, per un valor fix de $v_0$, l'abast serà màxim per a un angle de tir de 45 °. D'altra banda, com $\sin 2(90^o-{\theta }_0)=\sin 2{\theta }_0$, s'obté el mateix abast per a un angle de tir donat i per a la seva complementari.

Moviment balístic amb fricció

Fregament-k_wv. Trajectòries gairebé parabòliques amb fregament proporcional a la velocitat, per a cinc valors diferents de la velocitat horitzontal β = 1,5, β = 2,5, β = 2,5 i β = 1,5, des d'una altura h = 7δ .

La presència en el medi d'un fluid, com l'aire, exerceix un força de fregament que depèn del mòdul de la velocitat i és de sentit oposat a aquesta. En aquestes condicions, el moviment d'una partícula en un camp gravitatori uniforme no segueix estrictament una paràbola i és només gairebé-parabòlic. Pel que fa a la forma del fregament es distingeixen dos casos.

Moviment a baixa velocitat

Per a un fluid en repòs i un cos movent-se a molt baixa velocitat, el flux al voltant del cos pot considerar laminar i, en aquest cas, el fregament és proporcional a la velocitat. L'equació de la trajectòria resulta ser:

Plantilla:Equació on:

$H_0$ és l'altura inicial des de la qual cau el cos.

$\mathrm{\Delta }=g{m}^2/k_w^2,\beta =v_x{k}_w/mg$ són dos paràmetres que defineixen el problema en termes de les magnituds del problema.

$M,g,k_w,v_x$ són la massa del cos que cau, l'acceleració de la gravetat, el coeficient de fregament i la velocitat horitzontal inicial.

Per a alçades prou grans el fregament de l'aire fa que el cos caigui segons una trajectòria l'últim tram és pràcticament vertical, en ser frenada gairebé completament la velocitat horitzontal inicial.

Fregament-C_wv². Trajectòries gairebé parabòliques amb fregament proporcional a la velocitat, per a cinc valors diferents de la velocitat horitzontal β = 1,5, β = 2,5, β = 3,5 i β = 1,5, des d'una altura h = 7δ .

Moviment a velocitat moderada o gran

A velocitats moderadament grans o grans, o quan el fluid està en moviment, el flux al voltant del cos és turbulent i es produeixen remolins i pressions que generen una força de frenat proporcional al quadrat de la velocitat.

En lloc de les equacions anteriors, més difícils d'integrar, es pot usar en forma aproximada les següents equacions: Plantilla:Equació Per a aquestes equacions la trajectòria ve donada per: Plantilla:EquacióOn:

$H_0$ és l'altura inicial des de la qual cau el cos.

$\mathrm{\Delta }=1/C_w,\beta =\sqrt{g/(C_w{v}_x^2)}$ són dos paràmetres que defineixen el problema en termes de les magnituds del problema.

$G,C_w,v_x$ són l'acceleració de la gravetat, el coeficient de fregament i la velocitat horitzontal inicial.

Bibliografia

• Plantilla:Ref-llibre
• Plantilla:Ref-llibre
• Plantilla:Ref-llibre
• " Balística Exterior ", Francisco Pérez, Ministeri de Defensa, 1992.

Vegeu també

• Cinemàtica

Enllaços externs

• Full per calcular la distància i el temps de vol i poder comprendre les equacions anteriors