Teorema de Siacci

En cinemàtica, l'acceleració d'una partícula que es mou al llarg d'una corba en l'espai, és la derivada de la seva velocitat respecte el temps. En moltes aplicacions, el vector acceleració es presenta con la suma del seus components normal i tangencial que son ortogonals entre si. El teorema de Siacci, formulat pel matemàtic italià Francesco Siacci, és la descomposició cinemàtica del vector acceleració en els seus components radial i tangencial.Plantilla:Sfn En general, els components radial i tangencial no son ortogonals entre si. El teorema de Siacci és particularment útil en els moviments que tenen moment angular constant.

El teorema de Siacci en el pla

Moviment d'una partícula P en un pla.

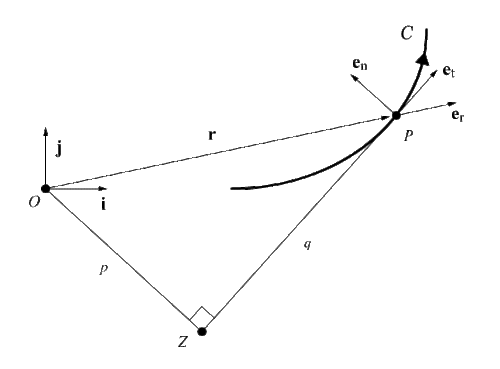
Sigui una partícula $P$ de massa $m$ movent-se en un espai euclidià bidimensional (moviment pla). Suposem que $C$ és la corba traçada per $P$ i $s$ és la longitud del arc de la corba $C$ corresponent al moment $t$. Sigui $O$ un punt d'origen arbitrari en el pla i els vectors $i,j$ estan fixats de forma ortonormal. La posició del vector de la partícula és:

$𝐫=r{𝐞}_r.$

El vector unitari $e_r$ és el vector radial bàsic d'un sistema de coordenades polars en el pla. El vector velocitat de la partícula és:

$𝐯=\frac{d𝐫}{dt}=\dot{s}{𝐞}_t=v{𝐞}_t,$

on $e_t$ és el vector unitari tangent a $C$. Definim el moment angular de $P$ com

$𝐡=𝐫\times m𝐯=h𝐤,$

on $k=i\times j$. Assumim que $h\ne 0$. La posició del vector $r$ es pot expressar, doncs, així

$𝐫=q{𝐞}_t-p{𝐞}_n$

segons les fórmules de Frenet-Serret $e_t,e_n,e_b$. La magnitud del moment angular és $h=mpv$, on $p$ és la perpendicular des de l'origen a la tangent $ZP$. D'acord amb el teorema de Siacci, l'acceleració $a$ de $P$ es por expressar com

$𝐚=-\frac{\kappa v^{2}r}{p}{𝐞}_r+\frac{(h^2{)}^{\prime }}{2p^2}{𝐞}_t=S_r{𝐞}_r+S_t{𝐞}_t.$

on el primer terme denota la diferencicació respecte l'arc $s$ i $\kappa$ és la funció de curvatura de la corba $C$. En general, $S_r$ i $S_t$ no son iguals a les projeccions ortogonals sobre $e_r$ i $e_t$.Plantilla:Sfn

El teorema de Siacci en l'espai

El teorema de Siacci es pot estendre als moviments en tres dimensions to three-dimensional motions. Sigui $C$ un espai corbat traçat per $P$ i $s$ la longitud de l'arc de $C$ corresponent al moment $t$. També, suposem que el component binormal del moment angular no és zero. Aleshores, el vector d'acceleració de $P$ es pot expressar com

$𝐚=-\frac{\kappa v^{2}r}{p}{𝐞}_r+(v\frac{dv}{ds}+\frac{\kappa v^{2}q}{p}){𝐞}_t.$

El component tangencial és tangent a la corba $C$. El component radial es dirigeix des del punt $P$ al punt en què la perpendicular des de l'origen arbitrari es troba amb el pla osculatriu.Plantilla:Sfn

Bibliografia

• Plantilla:Ref-publicació
• Plantilla:Ref-llibre
• Plantilla:Ref-llibre