Nombre de Fibonacci

Una tessel·lació de quadrats amb longitud de costat igual als nombres de la successió de Fibonacci: 1, 1, 2, 3, 5, 8, 13 i 21.

En matemàtiques, els nombres de Fibonacci, sovint denotats Plantilla:Math, formen una sèrie, anomenada successió de Fibonacci, tal que cada nombre de la sèrie és la suma dels dos nombres anteriors, prenent com a valors inicials de la sèrie 0 i 1. És a dir,Plantilla:Sfn $$F_0=0,F_1=1,$$ i $$F_n=F_{n-1}+F_{n-2}$$ per Plantilla:Math.

La seqüència comença: $$0,1,1,2,3,5,8,13,21,34,55,89,144,\dots$$

Si se segueixen definicions més antigues, el valor

$F_0=0$

és omès. Així doncs, la seqüència comença amb

$F_1=F_2=1,$

i la relació de recurrència

$F_n=F_{n-1}+F_{n-2}$

és vàlida per Plantilla:Math.Plantilla:SfnPlantilla:Sfn En la seva definició original, Fibonacci començava la seqüència amb

$F_1=1,F_2=2$

L'espiral de Fibonacci: una aproximació de l'espiral àuria creada en dibuixar arcs circulars que connecten els vèrtexs oposats de quadrats que segueixen la tessel·lació de Fibonacci; (vegeu la imatge superior)

Els nombres de Fibonacci estan estretament relacionats amb la secció àuria: la fórmula de Binet expressa l'Plantilla:Mvarèssim nombre de Fibonacci en termes de Plantilla:Mvar i la secció àuria, i implica que la raó de dos nombres consecutius de Fibonacci tendeix a la secció àuria a mesura que Plantilla:Mvar augmenta.

Els nombres de Fibonacci duen el nom del matemàtic italià Leonardo de Pisa, posteriorment conegut com Fibonacci. En el seu llibre de 1202 Liber Abaci, Fibonacci va introduir la sèrie a les matemàtiques europees occidentals,Plantilla:Sfn tot i que la seqüència ja havia estat descrita prèviament a l'Índia, al voltant de l'any 200 abans de Crist en una obra de Pingala quan enumerava possibles patrons en la poesia en sànscrit formats per síl·labes de dues longituds diferents.

Els nombres de Fibonacci apareixen de forma inesperada en les matemàtiques, fins a tal punt que hi ha un revista sencera dedicada al seu estudi, la Fibonacci Quarterly. Les aplicacions dels nombres de Fibonacci inclouen algorismes computacionals com la tècnica de cerca de Fibonacci i l'estructura de dades del monticle de Fibonacci, i grafs anomenats cubs de Fibonacci, que serveixen per interconnectar sistemes paral·lels i distribuïts.

També apareixen en patrons de la natura, com ara en el brancatge dels arbres, la distribució de les fulles del tronc, els brots de fruits en les pinyes, la floració de les carxoferes, l'obertura de les falgueres, i la distribució de les bràctees de les pinyes.

Els nombres de Fibonacci també estan molt relacionats amb els nombres de Lucas $L_n$, en el sentit que els nombres de Fibonacci i els de Lucas formen una parella completa de sèries de Lucas: $U_n(1,-1)=F_n$ and $V_n(1,-1)=L_n$.

Història

Tretze (F₇) maneres d'ordenar síl·labes llargues (mostrades com blocs vermells) i curtes (representades amb quadrats grisos) en una cadència de longitud sis. Cinc (F₅) acaben amb una síl·laba llarga i vuit (F₆) ho fan amb una síl·laba curta.

La sèrie de Fibonacci apareix en les matemàtiques a l'Índia en relació al prosòdia en sànscrit, tal com va assenyalar Parmanand Singh l'any 1986.Plantilla:Sfn En la tradició poètica en sànscrit, era interessant enumerar tots els patrons de síl·labes llarges (L) de 2 unitats de duració, juxtaposades amb les síl·labes curtes (C) d'1 unitat de durada. El recompte dels diferents patrons d'L i d'S successius d'una durada total fixa dona lloc als nombres de Fibonacci: el nombre de patrons de durada Plantilla:Math unitats és Plantilla:Math.

Hi ha consciència per primer cop del coneixement de la sèrie de Fibonacci en l'obra de Pingala (circa  450 –200 aC). Singh va citar la críptica fórmula de Pingala coneguda com misrau cha ("les dues es barregen") i els acadèmics van interpretar-ho en aquest context com: el nombre de patrons d'Plantilla:Math blocs (Plantilla:Math) s'obté afegint una [C] als Plantilla:Math casos i una [L] als Plantilla:Math casos. Bharata Muni també va demostrar conèixer la sèrie a Natya Shastra (c. 100 aC–c. 350 dC). Tanmateix, l'exposició més clara de la seqüència es troba en l'obra de Virahanka (c. 700 dC), l'obra del qual es va perdre però es pot trobar en una citació de Gopala (c. 1135):Plantilla:Sfn

Variacions de dos metres anteriors [és la variació]... Per exemple, per [un metre de longitud] quatre, variacions de metres de dos [i] tres són sumats, apareix el cinc. [calcula els exemples de 8, 13, 21]... D'aquesta manera, s'hauria de seguir el procés en totes les mātrā-vṛttas [combinacions prosòdiques].Plantilla:Efn

Hemachandra (al voltant de  1150) és també considerat sabedor de la seqüència, ne escriure que "la suma entre l'anterior i el d'abans és el nombre ... del següent mātrā-vṛtta."Plantilla:Sfn

Una pàgina del llibre de Liber Abaci de Fibonacci de la Biblioteca Nacional Central de Florència que mostra (en un requadre vermell) la seqüència de Fibonacci amb la posició en la sèrie etiquetada en nombres llatins i romans i el valor en nombres aràbics.

El nombre de parelles de conills de la seqüència de Fibonacci

Fora de l'Índia, la seqüència de Fibonacci va aparèixer per primer cop al Liber Abaci (El Llibre del Càlcul, 1202) de FibonacciPlantilla:Sfn on s'utilitzava per calcular el creixement en la població de conills. Fibonacci va considerar el creixement d'una població de conills ideal (biològicament poc realista), assumint que: una parella de cries de conill nounada es posen en un camp; cada parella de cries s'aparella a l'edat d'un mes, i al final del segon mes sempre produeixen una altra parella de conills; i els conills mai no moren, sinó que continuen criant per sempre. Fibonacci va proposar aquest enigma: quantes parelles hi haurà en un any?

• Al final del primer mes, s'aparellen, però hi segueix havent només una parella.
• Al final del segon mes produeixen una nova parella, així doncs hi ha 2 parelles en el camp.
• Al final del tercer mes, la parella original produeix una segona parella, però la segona parella simplement s'aparellen sense criar, així doncs hi ha 3 parelles en total.
• Al final del quart mes, la parella original ha produït una altra parella, i la parella que va néixer fa dos mesos produeixen la seva primera parella, fent-ne un total de cinc.

Al final del mes Plantilla:Math-èssim, el nombre de parelles de conills és igual al nombre de parelles madures (és a dir, el nombre de parelles en el mes Plantilla:Math) més el nombre de parelles vives el mes anterior (el mes Plantilla:Math). El nombre en el mes Plantilla:Math-èssim és l'Plantilla:Math-èssim nombre de Fibonacci.

El terme "seqüència de Fibonacci" va ser utilitzat per primer cop pel teòric de nombres del Plantilla:Segle Édouard Lucas.

Propietats de la seqüència

Els primers 21 nombres de Fibonacci Plantilla:Math són:

F0	F1	F₂	F₃	F₄	F₅	F₆	F₇	F₈	F9	F10	F11	F₁₂	F13	F14	F15	F16	F17	F18	F19	F20
0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	610	987	1597	2584	4181	6765

La sèrie pot ser estesa a índexos negatius Plantilla:Math utilitzant la relació de recurrència reordenada

$$F_{n-2}=F_n-F_{n-1},$$

Plantilla:Anchor que dona lloc a la sèrie de nombres "negafibonacci" que satisfan $$F_{-n}=(-1{)}^{n+1}{F}_n.$$

Així doncs, la sèrie bidireccional queda

F−8

F−7

F−6

F−5

F−4

F−3

F−2

F−1

F0

F1

F₂

F₃

F₄

F₅

F₆

F₇

F₈

−21

13

−8

5

−3

2

−1

1

0

1

1

2

3

5

8

13

21

Relació amb la secció àuria

Expressió en forma tancada

Com tota seqüència definida a partir d'una recurrència lineal amb coeficients constants, els nombres de Fibonacci tenen una expressió en forma tancada. Ha estat coneguda com la fórmula de Binet, pel matemàtic francès Jacques Philippe Marie Binet, tot i que ja era coneguda per Abraham de Moivre i Daniel Bernoulli:

$$F_n=\frac{{\phi }^n-{\psi }^n}{\phi -\psi }=\frac{{\phi }^n-{\psi }^n}{\sqrt{5}},$$ on $$\phi =\frac{1+\sqrt{5}}{2}\approx 1.6180339887\dots$$ és la secció àuria Plantilla:OEIS, iPlantilla:Sfn $$\psi =\frac{1-\sqrt{5}}{2}=1-\phi =-\frac{1}{\phi }\approx -0.6180339887\dots .$$

Com que $\psi =-{\phi }^{-1}$, aquesta fórmula també pot ser escrita com $$F_n=\frac{{\phi }^n-(-\phi {)}^{-n}}{\sqrt{5}}=\frac{{\phi }^n-(-\phi {)}^{-n}}{2\phi -1}.$$ Per veure-ho,Plantilla:Sfn noti's quw Plantilla:Mvar i Plantilla:Mvar són totes dues solucions de les equacions $$x^2=x+1\text{and}{x}^n=x^{n-1}+x^{n-2},$$ així doncs, les potències de Plantilla:Mvar i Plantilla:Mvar satisfan la recursió de Fibonacci. En altres paraules, $${\phi }^n={\phi }^{n-1}+{\phi }^{n-2}$$ i $${\psi }^n={\psi }^{n-1}+{\psi }^{n-2}.$$

Segueix que per valors qualssevol de Plantilla:Math i de Plantilla:Math, la seqüència definida per $$U_n=a{\phi }^n+b{\psi }^n$$ satisfà la mateixa recurrència. $$U_{n-1}+U_{n-2}=a{\phi }^{n-1}+b{\psi }^{n-1}+a{\phi }^{n-2}+b{\psi }^{n-2}=a{\phi }^{n-1}+a{\phi }^{n-2}+b{\psi }^{n-1}+b{\psi }^{n-2}=U_n$$

Si Plantilla:Math i Plantilla:Math són triats tals que Plantilla:Math i Plantilla:Math llavors la seqüència resultant Plantilla:Math ha de ser una seqüència de Fibonacci. Això és el mateix que imposar que Plantilla:Math i Plantilla:Math satisfacin el sistema d'equacions: $$\{\begin{array}{c}a+b=0\\ \phi a+\psi b=1\end{array}$$ amb solució $$a=\frac{1}{\phi -\psi }=\frac{1}{\sqrt{5}},b=-a,$$ que produeix la fórmula imposada.

Prenent com a valors inicials Plantilla:Math i Plantilla:Math constants arbitràries, una solució més general és: $$U_n=a{\phi }^n+b{\psi }^n$$ on $$a=\frac{U_1-U_0\psi }{\sqrt{5}}$$ $$b=\frac{U_0\phi -U_1}{\sqrt{5}}.$$

Càlcul per arrodoniment

Com que $$\left|\frac{{\psi }^n}{\sqrt{5}}\right|<\frac{1}{2}$$

per tot Plantilla:Math, el nombre Plantilla:Math és l'enter més proper a $\frac{{\phi }^n}{\sqrt{5}}$. Per tant, es pot trobar arrodoniment, utilitzant la funció de l'enter més proper: $$F_n=\left[\frac{{\phi }^n}{\sqrt{5}}\right],n\ge 0.$$

De fet, l'error d'arrodoniment és molt petit, menys de 0.1 per Plantilla:Math, i més de 0.01 per Plantilla:Math.

També es poden calcular els nombres de Fibonacci mitjançant el truncament, en termes de la funció terra: $$F_n=\lfloor \frac{{\phi }^n}{\sqrt{5}}+\frac{1}{2}\rfloor ,n\ge 0.$$

Com que la funció terra és monòtona, es pot invertir aquesta darrera fórmula per trobar l'índex Plantilla:Math del major nombre de Fibonacci que no és més gran que un nombre real Plantilla:Math: $$n(F)=\lfloor {\log }_{\phi }(F\cdot \sqrt{5}+\frac{1}{2})\rfloor ,$$ on ${\log }_{\phi }(x)=\ln (x)/\ln (\phi )={\log }_{10}(x)/{\log }_{10}(\phi ).$

Límit de quocients consecutius

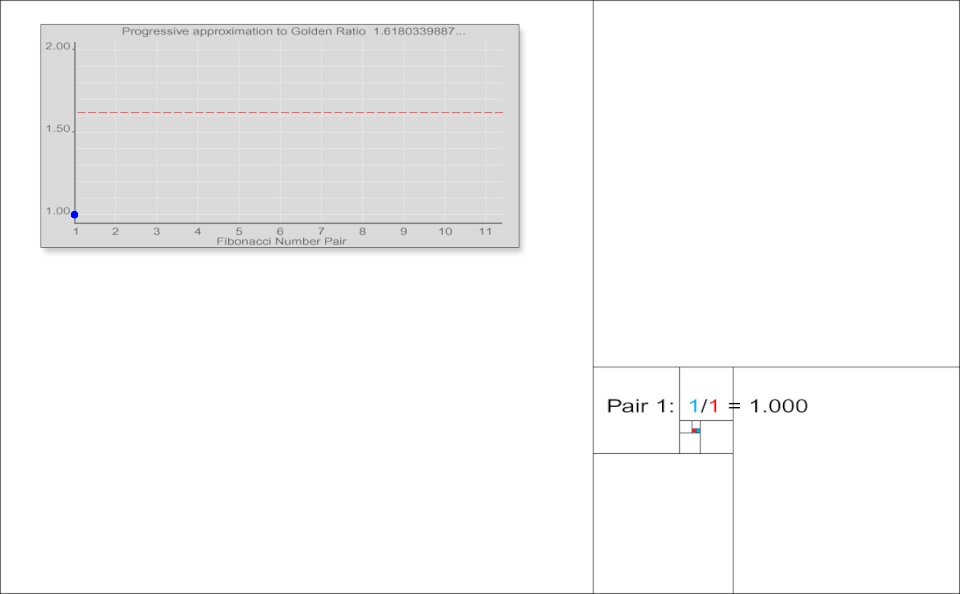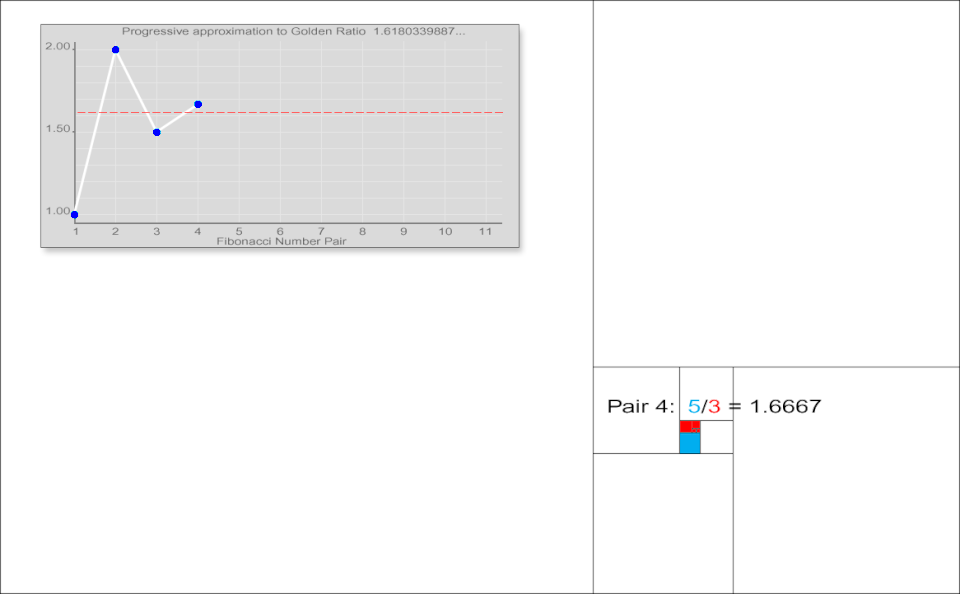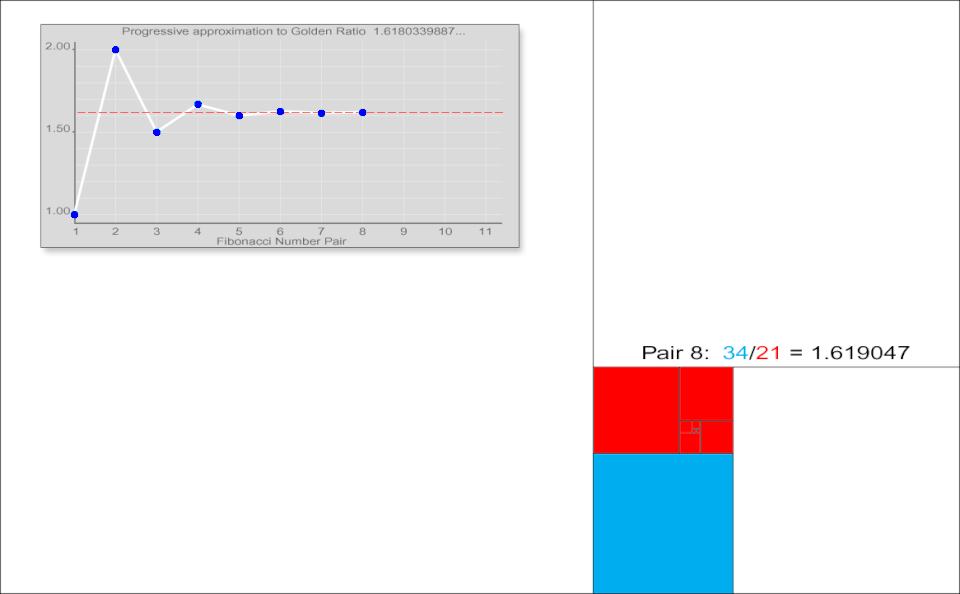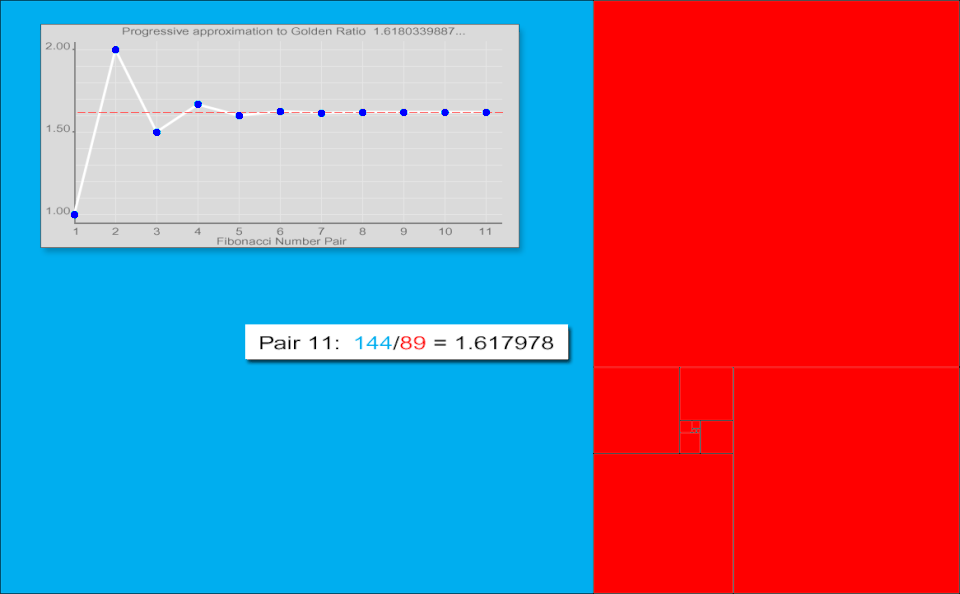
Tessel·lacions successives del pla i una gràfica de les aproximacions de la secció àuria calculades dividint cada nombre de Fibonacci per l'anterior

Johannes Kepler va observar que la raó entre nombres consecutius de Fibonacci convergeix. Va escriure que "el que 5 és a 8 és, pràcticament, el que 8 és a 13, i el que 8 és a 13, és el que 13 és a 21 gairebé", i va concloure que aquestes raons tendeixen a la secció àuria $\phi :$ $$\underset{n\to \mathrm{\infty }}{\lim }\frac{F_{n+1}}{F_n}=\phi .$$

Aquesta convergència funciona independentment dels valors inicials, exceptuant el cas trivial de 0,0, o qualsevol parella en la secció àuria conjugada, $-1/\phi .$ Això es pot verificar usant la fórmula de Binet. Per exemple, els valors inicials de 3 i 2 generen la seqüència 3, 2, 5, 7, 12, 19, 31, 50, 81, 131, 212, 343, 555, ... La raó de termes consecutius en aquesta seqüència mostra la mateixa convergència cap a la secció àuria.

Descomposició en potències

Com que la secció àuria satisfà l'equació $${\phi }^2=\phi +1,$$

es pot utilitzar aquesta expressió per descompondre potències més elevades ${\phi }^n$ com a funció lineal de potència més baixes, que alhora poden ser descomposades successivament fins a obtenir una combinació lineal de $\phi$ i 1. La relació de recurrència resultant acaben tenint nombres de Fibonacci com a coeficinets lineals: $${\phi }^n=F_n\phi +F_{n-1}.$$ Es pot demostrar aquesta equació mitjançant inducció en n.

Aquesta expressió és també vàlida per n < 1 si s'esté la seqüència de Fibonacci F_n als enters negatius, utilitzant la relació de Fibonacci $F_n=F_{n-1}+F_{n-2}.$

Forma matricial

Un sistema de dues dimensions d'equacions de diferència que descriu la seqüència de Fibonacci és

$$(\genfrac{}{}{0ex}{}{F_{k+2}}{F_{k+1}})=\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)(\genfrac{}{}{0ex}{}{F_{k+1}}{F_k})$$ denotat, alternativament, com $${\overrightarrow{F}}_{k+1}=𝐀{\overrightarrow{F}}_k,$$

que implica ${\overrightarrow{F}}_n={𝐀}^n{\overrightarrow{F}}_0$. Els valors propis de la matriu Plantilla:Math són $\phi =\frac{1}{2}(1+\sqrt{5})$ i $-{\phi }^{-1}=\frac{1}{2}(1-\sqrt{5})$ que corresponen als vectors propis $$\overrightarrow{\mu }=(\genfrac{}{}{0ex}{}{\phi }{1})$$ i $$\overrightarrow{\nu }=(\genfrac{}{}{0ex}{}{-{\phi }^{-1}}{1}).$$ Com que els valors inicials són $${\overrightarrow{F}}_0=(\genfrac{}{}{0ex}{}{1}{0})=\frac{1}{\sqrt{5}}\overrightarrow{\mu }-\frac{1}{\sqrt{5}}\overrightarrow{\nu },$$ es té que el terme Plantilla:Mvar-èssim és $$\begin{array}{cc}{\overrightarrow{F}}_n& =\frac{1}{\sqrt{5}}{A}^n\overrightarrow{\mu }-\frac{1}{\sqrt{5}}{A}^n\overrightarrow{\nu }\\ & =\frac{1}{\sqrt{5}}{\phi }^n\overrightarrow{\mu }-\frac{1}{\sqrt{5}}(-\phi {)}^{-n}\overrightarrow{\nu }\\ & =\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n(\genfrac{}{}{0ex}{}{\phi }{1})-\frac{1}{\sqrt{5}}{\left(\frac{1-\sqrt{5}}{2}\right)}^n(\genfrac{}{}{0ex}{}{-{\phi }^{-1}}{1}),\end{array}$$ D'aquesta expressió, es pot concloure que l'element Plantilla:Mvar-èssim de la sèrie de Fibonacci pot ser obtingut de manera directa a partir de l'expressió en forma tancada: $$F_n=\frac{1}{\sqrt{5}}{\left(\frac{1+\sqrt{5}}{2}\right)}^n-\frac{1}{\sqrt{5}}{\left(\frac{1-\sqrt{5}}{2}\right)}^n.$$

De manera equivalent, es pot fer el mateix càlcul diagonalitzant Plantilla:Math a partir de l'ús de la seva descomposició en valors propis: $$\begin{array}{cc}A& =S\mathrm{\Lambda }{S}^{-1},\\ A^n& =S{\mathrm{\Lambda }}^n{S}^{-1},\end{array}$$ on $\mathrm{\Lambda }=\left(\begin{array}{cc}\phi & 0\\ 0& -{\phi }^{-1}\end{array}\right)$ i $S=\left(\begin{array}{cc}\phi & -{\phi }^{-1}\\ 1& 1\end{array}\right).$ L'expressió en forma tancada de l'element Plantilla:Mvar-èssim de la sèrie de Fibonacci ve, doncs, donat per

$$\begin{array}{cc}(\genfrac{}{}{0ex}{}{F_{n+1}}{F_n})& =A^n(\genfrac{}{}{0ex}{}{F_1}{F_0})\\ & =S{\mathrm{\Lambda }}^n{S}^{-1}(\genfrac{}{}{0ex}{}{F_1}{F_0})\\ & =S\left(\begin{array}{cc}{\phi }^n& 0\\ 0& (-\phi {)}^{-n}\end{array}\right)S^{-1}(\genfrac{}{}{0ex}{}{F_1}{F_0})\\ & =\left(\begin{array}{cc}\phi & -{\phi }^{-1}\\ 1& 1\end{array}\right)\left(\begin{array}{cc}{\phi }^n& 0\\ 0& (-\phi {)}^{-n}\end{array}\right)\frac{1}{\sqrt{5}}\left(\begin{array}{cc}1& {\phi }^{-1}\\ -1& \phi \end{array}\right)(\genfrac{}{}{0ex}{}{1}{0}),\end{array}$$

que implica, com abans, $$F_n=\frac{{\phi }^n-(-\phi {)}^{-n}}{\sqrt{5}}.$$

La matriu Plantilla:Math té determinant de −1 i, per tant, és una matriu unimodular 2×2.

Es pot entendre aquesta propietat en termes de la representació en fracció contínua de la secció àuria:

$$\phi =1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\ddots }}}.$$

Els nombres de Fibonacci apareixen a mesura que la raó de convergents successius de la fracció contínua de Plantilla:Mvar, i la matriu formada a partir del convergents successius de qualsevol fracció contínua té un determinant de +1 o −1. La representació matricial dona la següent expressió en forma tancada dels nombres de Fibonacci:

$${\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right)}^n=\left(\begin{array}{cc}{F}_{n+1}& F_n\\ F_n& F_{n-1}\end{array}\right).$$

Prenent el determinant en ambdós costats de l'equació, s'obté la identitat de Cassini, $$(-1{)}^n=F_{n+1}{F}_{n-1}-F_n^2.$$

A més, com que Plantilla:Math per qualsevol matriu quadrada Plantilla:Math, es poden derivar les següents identitats (s'obtenen a partir de dos coeficients diferents del producte matricial, i es pot deduir fàcilment la segona a partir de la primera canviant Plantilla:Math per Plantilla:Math), $$\begin{array}{cc}{F}_m{F}_n+F_{m-1}{F}_{n-1}& =F_{m+n-1},\\ F_m{F}_{n+1}+F_{m-1}{F}_n& =F_{m+n}.\end{array}$$

En particular, amb Plantilla:Math, $$\begin{array}{cc}{F}_{2n-1}& =F_n^2+F_{n-1}^2\\ F_{2n}& =(F_{n-1}+F_{n+1})F_n\\ & =(2F_{n-1}+F_n)F_n\\ & =(2F_{n+1}-F_n)F_n.\end{array}$$

Aquestes últimes dues identitats proporcionen un mètode per calcular els nombres de Fibonacci recursivament en Plantilla:Math operacions aritmètiques i en temps Plantilla:Math, on Plantilla:Math és el temps que es triga a multiplicar dos nombres d'Plantilla:Math dígits. Això coincideix amb el temps de calcular l'Plantilla:Math-éssim nombre de Fibonacci a partir de la fórmula matricial en forma tancada, però amb menys passos redundants si s'evita tornar a calcular un nombre de Fibonacci que ja s'havia calculat (recursió amb memoització).

Identificació

Hom es pot preguntar si un enter positiux és un nombre de Fibonacci. Això és veritat si i només si almenys un dels dos nombres $5x^2+4$ i $5x^2-4$ és un quadrat perfecte. Això és perquè es pot reordenar la fórmula de Binet de més amunt fins a tenir

$$n={\log }_{\phi }\left(\frac{F_n\sqrt{5}+\sqrt{5F_n^2\pm 4}}{2}\right),$$

que permet trobar la posició en la seqüència d'un nombre de Fibonacci.

Aquesta fórmula ha de tornar un enter per tot n, així que l'expressió radical ha de ser un enter (altrament, el logaritme ni tan sols retorn un nombre racional).

Identitats combinatòries

Demostracions combinatòries

La majoria de les identitats relacionades amb els nombres de Fibonacci poden ser demostrades a partir d'arguments basats en combinatòria que utilitzen el fet que es pot interpretar F_n com el nombre de seqüències d'1s i 2s que sumen n − 1. Això es pot rendre com la definició de F_n, amb el conveni que F₀ = 0, en el sentit que no hi ha cap suma que dongui −1, i que F₁ = 1, en el sentit que la suma buida "suma" 0. Aquí, l'ordre dels sumands importa. Per exemple, 1 + 2 i 2 + 1 es consideren sumes diferents.

Per exemple, la relació recursiva

$F_n=F_{n-1}+F_{n-2},$

o, en altres paraules, el nombre de Fibonacci n-èssim és la suma dels dos nombres de Fibonacci previs, es pot mostrar dividint les F_n sumes d'1s i 2s que sumen n − 1 en dos grups que no se solapen. Un dels grups conté les sumes el primer terme dels quals és 1 i l'altre conté les sumes que tenen el 2 com a primer terme. En el primer grup, la resta de termes sumen n − 2, així que hi ha F_n-1 sumes, i en el segon grup la resta de termes sumen n − 3, així doncs hi ha F_n−2 sumes. Així doncs, hi ha un total de F_n−1 + F_n−2 sumes en total, que és igual a F_n.

De manera similar, es pot demostrar que la suma dels primers nombres de Fibonacci fins al terme n-èssim és igual al nombre de Fibonacci (n + 2)-èssim menys u.Plantilla:Sfn En símbols: $$\sum _{i=1}^n{F}_i=F_{n+2}-1$$

Això es fa dividint les sumes que donguin n + 1 d'una forma diferent, aquest cop a partir de la ubicació del primer 2. Específicament, el primer grup consisteix en aquelles sumes que comencen amb un 2, el segon grup és el de les sumes que comencen per un 1 + 2, el tercer és 1 + 1 + 2, i així successivament, fins a l'últim grup, que consisteix en l'única suma en què només hi ha 1s. El nombre de sumes en el primer grup és F(n), F(n − 1) en el segon grup, i així successivament, amb 1 suma en l'últim grup. Així doncs, el nombre total de sumes és F(n) + F(n − 1) + ... + F(1) + 1 i, per tant, aquesta quantitat és igual a F(n + 2).

Un argument similar, agrupant les sumes a partir de la posició del primer 1 enlloc de la posició del primer 2, dona dues més identitats: $$\sum _{i=0}^{n-1}{F}_{2i+1}=F_{2n}$$ i $$\sum _{i=1}^n{F}_{2i}=F_{2n+1}-1.$$ En paraules, la suma dels primers nombres de Fibonacci d'índex senar fins a F_2n−1 és el nombre de Fibonacci (2n)-èssim, i la suma dels primers nombres de Fibonacci d'índex parell fins a F_2n és el nombre de Fibonacci (2n + 1)-èssim menys  1.

Es pot utilitzar un truc diferent per demostrar $$\sum _{i=1}^n{F_i}^2=F_n{F}_{n+1},$$ o en paraules, la suma dels quadrats dels primers nombres de Fibonacci fins a F_n és el producte dels nombres de Fibonacci n-èssim i (n + 1)-èssim. En aquest cas, es pot descompondre un rectangle de Fibonacci de costats F_n i F(n + 1) en quadrats de mida F_n, F_n−1, i així successivament fins a F₁ = 1, pel qual la identitat segueix a partir de comparar les àrees (vegi's la primera figura a dalt de tot de l'article).

Mètode simbòlic

També es considera la seqüència $(F_n{)}_{n\in \mathbb{N}}$ utilitzant el mètode simbòlic. Més precisament, aquesta seqüència correspon a una classe combinatòria especificable. L'especificació d'aquesta seqüència és $\mathrm{Seq}(𝒵\mathcal{+}{𝒵}^2)$. En efecte, com s'ha afrimat més amunt, el nombre de Fibonacci $n$-èssim és igual al nombre de composició combinatòria de $n-1$ utilitzant els termes 1 i 2.

Segueix que la funció generadora ordinària de la seqüència de Fibonacci, és a dir $\sum _{i=0}^{\mathrm{\infty }}{F}_i{z}^i$, és la funció complexa $\frac{z}{1-z-z^2}$.

Demostracions per inducció

Sovint es poden demostrar fàcilment les identitats de Fibonacci utilitzant la inducció matemàtica.

Per exemple, reconsideri's

$\sum _{i=1}^n{F}_i=F_{n+2}-1$

Sumant $F_{n+1}$ a tots dos costats de la igualtat

$\sum _{i=1}^n{F}_i+F_{n+1}=F_{n+1}+F_{n+2}-1$

es té la fórmula per $n+1$

$\sum _{i=1}^{n+1}{F}_i=F_{n+3}-1$

De manera similar, si se suma $F_{n+1}^2$ a tots dos costats de la igualtat

$\sum _{i=1}^n{F_i}^2=F_n{F}_{n+1}$

s'obté

$\sum _{i=1}^n{F_i}^2+F_{n+1}^2=F_{n+1}(F_n+F_{n+1})$

$\sum _{i=1}^{n+1}{F_i}^2=F_{n+1}{F}_{n+2}$

Demostracions de la fórmula de Binet

La fórmula de Binet és

$\sqrt{5}{F}_n={\varphi }^n-{\psi }^n$

Això es pot utilitzar per demostrar les identitats de Fibonacci.

Per exemple, per demostrar que ${\sum }_{i=1}^n{F}_i=F_{n+2}-1$

noti's que el costat esquerre de la igualtat multiplicat per $\sqrt{5}$ es converteix en

$1+\varphi +{\varphi }^2+\dots +{\varphi }^n-(1+\psi +{\psi }^2+\dots +{\psi }^n)$

$=\frac{{\varphi }^{n+1}-1}{\varphi -1}-\frac{{\psi }^{n+1}-1}{\psi -1}$

$=\frac{{\varphi }^{n+1}-1}{-\psi }-\frac{{\psi }^{n+1}-1}{-\varphi }$

$=\frac{-{\varphi }^{n+2}+\varphi +{\psi }^{n+2}-\psi }{\varphi \psi }$

Com que $\varphi \psi =-1$ i $\varphi -\psi =\sqrt{5}$, es té que

$={\varphi }^{n+2}-{\psi }^{n+2}-(\varphi -\psi )$

$=\sqrt{5}(F_{n+2}-1)$

com es volia.

Altres identitats

Es poden derivar diverses altres identitats utilitzant diferents mètodes. Aquí hi ha algunes d'elles:

Identitats de Cassini i Catalan

La identitat de Cassini afirma que

$F_n^2-F_{n+1}{F}_{n-1}=(-1{)}^{n-1}$

La identitat de Catalan n'és una generalització:

$F_n^2-F_{n+r}{F}_{n-r}=(-1{)}^{n-r}{F}_r^2$

Identitats de d'Ocagne

Les identitats de d'Ocagne són les següents

$F_m{F}_{n+1}-F_{m+1}{F}_n=(-1{)}^n{F}_{m-n}$

$F_{2n}=F_{n+1}^2-F_{n-1}^2=F_n(F_{n+1}+F_{n-1})=F_n{L}_n$

on L_n és l'n-èssim nombre de Lucas. La segona és una identitat relacionada amb el terme 2n de la successió; altres identitats d'aquest tipus són

$F_{3n}=2F_n^3+3F_n{F}_{n+1}{F}_{n-1}=5F_n^3+3(-1{)}^n{F}_n$

mitjançant la identitat de Cassini.

$F_{3n+1}=F_{n+1}^3+3F_{n+1}{F}_n^2-F_n^3$

$F_{3n+2}=F_{n+1}^3+3F_{n+1}^2{F}_n+F_n^3$

$F_{4n}=4F_n{F}_{n+1}(F_{n+1}^2+2F_n^2)-3F_n^2(F_n^2+2F_{n+1}^2)$

Aquestes es poden obtenir experimentalment utilitzant reducció de reticle, i són útils per establir un crivell especial del cos de nombres per factoritzar un nombre de Fibonacci.

Més generalment,

$F_{kn+c}=\sum _{i=0}^k(\genfrac{}{}{0ex}{}{k}{i})F_{c-i}{F}_n^i{F}_{n+1}^{k-i}.$

o, alternativament,

$F_{kn+c}=\sum _{i=0}^k(\genfrac{}{}{0ex}{}{k}{i})F_{c+i}{F}_n^i{F}_{n-1}^{k-i}.$

Si es fixa Plantilla:Math en aquesta fórmula, es tornen a obtenir les fórmules del final de la secció de més amunt Forma matricial.

Funció generatriu

La funció generatriu de la seqüència de Fibonacci és la sèrie de potències

$s(x)=\sum _{k=0}^{\mathrm{\infty }}{F}_k{x}^k=\sum _{k=1}^{\mathrm{\infty }}{F}_k{x}^k=0+x+x^2+2x^3+3x^4+\dots .$

Aquesta sèrie és convergent per $|x|<\frac{1}{\phi },$ i la seva suma té una forma tancada simple:

$s(x)=\frac{x}{1-x-x^2}$

Això es pot demostrar utilitzant la recurrència de Fibonacci expandint cada coeficient en una suma infinita: $$\begin{array}{cc}s(x)& =\sum _{k=0}^{\mathrm{\infty }}{F}_k{x}^k\\ & =F_0+F_{1}x+\sum _{k=2}^{\mathrm{\infty }}{F}_k{x}^k\\ & =F_0+F_{1}x+\sum _{k=2}^{\mathrm{\infty }}(F_{k-1}+F_{k-2})x^k\\ & =x+\sum _{k=2}^{\mathrm{\infty }}{F}_{k-1}{x}^k+\sum _{k=2}^{\mathrm{\infty }}{F}_{k-2}{x}^k\\ & =x+x\sum _{k=2}^{\mathrm{\infty }}{F}_{k-1}{x}^{k-1}+x^2\sum _{k=2}^{\mathrm{\infty }}{F}_{k-2}{x}^{k-2}\\ & =x+x\sum _{k=1}^{\mathrm{\infty }}{F}_k{x}^k+x^2\sum _{k=0}^{\mathrm{\infty }}{F}_k{x}^k\\ & =x+xs(x)+x^{2}s(x).\end{array}$$

Resolent l'equació

$s(x)=x+xs(x)+x^{2}s(x)$

per s(x) resulta en la forma tancada.

$-s(-\frac{1}{x})$ dona la funció generatriu pels nombres negafibonacci, i $s(x)$ satisfà l'equació funcional

$s(x)=s(-\frac{1}{x})$.

La descomposició en fraccions parcials ve donada per

$s(x)=\frac{1}{\sqrt{5}}(\frac{1}{1-\phi x}-\frac{1}{1-\varphi x})$

on $\phi =\frac{1+\sqrt{5}}{2}$ és la secció àuria i $\varphi =\frac{1-\sqrt{5}}{2}$ és el seu conjugat.

Vegeu també

• Constant d'Embree-Trefethen
• Nombres de Lucas

Referències

Obra citada

• Plantilla:Citar ref.
• Plantilla:Citar ref.
• Plantilla:Citar ref.
  • Plantilla:Citar ref.
• Plantilla:Citar ref.
• Plantilla:Ref-llibre
• Plantilla:Citar ref.
• Plantilla:Citar ref