Equació d'Eckhaus

i ψ_{t} + ψ_{x x} + 2 {(| ψ |^{2})}_{x} ψ + | ψ |^{4} ψ = 0 .

L'equació va ser introduïda de forma independent per Wiktor Eckhaus i per Anjan Kundu per modelar la propagació de les ones en medis dispersius.Plantilla:Sfn Plantilla:Sfn L'equació de Kundu-Eckhaus admet molts tipus diferents de solucions analítiques (igual que l'equació no-lineal de Schrödinge), incloent, però sense limitar-se, les solucions racionals d'onades gegants.Plantilla:Sfn El comportament de les seves solucions estocàstiques d'onada gegant i els seus espectres es poden utilitzar amb finalitats de detecció precoç.Plantilla:Sfn

Linealització

i φ_{t} + φ_{x x} = 0,

mitjançant la transformació no-lineal:Plantilla:Sfn

φ (x, t) = ψ (x, t) \exp (\int_{- \infty}^{x} | ψ (x^{'}, t) |^{2} d x^{'}) .

La transformació inversa és:

ψ (x, t) = \frac{φ (x, t)}{{(1 + 2 \int_{- \infty}^{x} | φ (x^{'}, t) |^{2} d x^{'})}^{1 / 2}} .

Aquesta linealització també implica que l'equació d’Eckhaus és integrable.

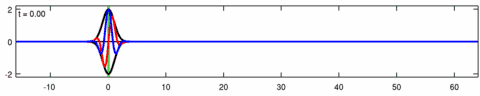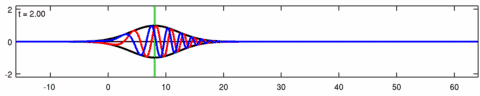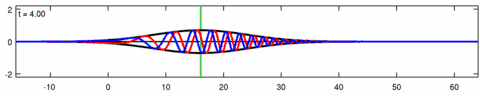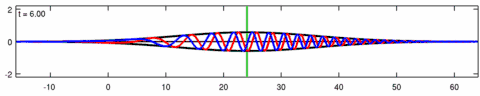
Animació d'una solució de paquets d'ones de lPlantilla:'equació d'Eckhaus. La línia blava és la part real de la solució, la línia vermella és la part imaginària i la línia negra és l'embolcall d’ona (valor absolut). Tingueu en compte l’asimetria del sobre $| ψ (x, t) |$ per a l'equació d’Eckhaus, mentre que el sobre $| φ (x, t) |$ (de la solució corresponent a l'equació lineal de Schrödinger) és simètric (a $x$ ). Les ones curtes del paquet es propaguen més ràpidament que les ones llargues

Animació de la solució de paquets d’ones de l'equació lineal de Schrödinger (corresponent amb l’animació anterior per a l'equació d’Eckhaus). La línia blava és la part real de la solució, la línia vermella és la part imaginària, la línia negra és l'embolcall d’ona (valor absolut) i la línia verda és el centroide del paquet d’ona