Divisió de pols

La divisió de pols és un fenomen explotat en algunes formes de compensació de freqüència utilitzades en un amplificador electrònic. Quan s'introdueix un condensador entre els costats d'entrada i sortida de l'amplificador amb la intenció de moure el pol més baix en freqüència (generalment un pol d'entrada) a freqüències més baixes, la divisió del pol fa que el pol següent en freqüència (normalment un pol de sortida) es mogui a una freqüència més alta. Aquest moviment del pol augmenta l'estabilitat de l'amplificador i millora la seva resposta a l'esglaó a costa de la disminució de la velocitat.

Exemple de trencament de pols

Figura 1: Amplificador operacional amb condensador de compensació C _C entre entrada i sortida; Observeu que l'amplificador té una impedància d'entrada R _i i una impedància de sortida R _o. (editar: aquesta xifra és defectuosa, ja que els signes + i - s'han de canviar. Cal que hi hagi comentaris negatius.)

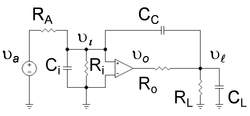
Aquest exemple mostra que la introducció del condensador denominat C_C a l'amplificador de la figura 1 té dos resultats: primer fa que el pol de freqüència més baixa de l'amplificador es mogui encara més baixa en freqüència i, segon, fa que el pol superior es mogui més alt en freqüència. L'amplificador de la figura 1 té un pol de baixa freqüència a causa de la resistència d'entrada afegida R_i i la capacitat C_i, amb la constant de temps C_i(R_A||R_i). Aquest pol es mou en freqüència cap avall per l'efecte Miller. A l'amplificador se li dóna un pol de sortida d'alta freqüència afegint la resistència de càrrega R_L i la capacitat C_L, amb la constant de temps C_L(R_o||R_L). El moviment ascendent del pol d'alta freqüència es produeix perquè el condensador de compensació amplificat per Miller C_C altera la dependència de la freqüència del divisor de voltatge de sortida.

Figura 2: Amplificador operacional amb condensador de compensació transformat mitjançant el teorema de Miller per substituir el condensador de compensació per un condensador de Miller a l'entrada i una font de corrent dependent de la freqüència a la sortida. (editar: aquesta xifra és defectuosa, ja que els signes + i - s'han de canviar. Cal que hi hagi comentaris negatius.)

El primer objectiu, mostrar el pol més baix es mou en freqüència cap avall, s'estableix utilitzant el mateix enfocament que l'article del teorema de Miller. Seguint el procediment descrit a l'article sobre el teorema de Miller, el circuit de la figura 1 es transforma al de la figura 2, que és elèctricament equivalent a la figura 1. L'aplicació de la llei actual de Kirchhoff al costat d'entrada de la figura 2 determina la tensió d'entrada $v_i$ a l'amplificador operacional ideal en funció de la tensió del senyal aplicada$v_a$, és a dir,

$\frac{v_i}{v_a}=\frac{R_i}{R_i+R_A}\frac{1}{1+j\omega (C_M+C_i)(R_A\Vert R_i)},$

que presenta un roll-off amb freqüència que comença a f ₁ on

$\begin{array}{cc}{f}_1& =\frac{1}{2\pi (C_M+C_i)(R_A\Vert R_i)}\\ & =\frac{1}{2\pi {\tau }_1}\\ \end{array}$

que introdueix la notació ${\tau }_1$ per a la constant de temps del pol més baix. Aquesta freqüència és inferior a la baixa freqüència inicial de l'amplificador, que per C_C = 0 F és $\frac{1}{2\pi C_i(R_A\Vert R_i)}$.

Passant al segon objectiu, mostrant que el pol més alt es mou encara més en freqüència, cal mirar el costat de sortida del circuit, que contribueix amb un segon factor al guany global i a la dependència addicional de la freqüència. La tensió $v_o$ ve determinat pel guany de l'amplificador operacional ideal dins de l'amplificador com

$v_o=A_v{v}_i.$

Utilitzant aquesta relació i aplicant la llei actual de Kirchhoff al costat de sortida del circuit es determina la tensió de càrrega $v_{\ell }$ en funció de la tensió $v_i$ a l'entrada de l'amplificador operacional ideal com:

$\frac{v_{\ell }}{v_i}=A_v\frac{R_L}{R_L+R_o}$$\cdot \frac{1+j\omega C_C{R}_o/A_v}{1+j\omega (C_L+C_C)(R_o\Vert R_L)}.$

Aquesta expressió es combina amb el factor de guany trobat anteriorment per al costat d'entrada del circuit per obtenir el guany global com

$\frac{v_{\ell }}{v_a}=\frac{v_{\ell }}{v_i}\frac{v_i}{v_a}$

$=A_v\frac{R_i}{R_i+R_A}\cdot \frac{R_L}{R_L+R_o}$$\cdot \frac{1}{1+j\omega (C_M+C_i)(R_A\Vert R_i)}$$\cdot \frac{1+j\omega C_C{R}_o/A_v}{1+j\omega (C_L+C_C)(R_o\Vert R_L)}.$

Aquesta fórmula de guany sembla mostrar una resposta simple de dos pols amb dues constants de temps. (També presenta un zero en el numerador, però, suposant que el guany de l'amplificador A_v és gran, aquest zero només és important a freqüències massa altes per importar en aquesta discussió, de manera que el numerador es pot aproximar com a unitat.) No obstant això, tot i que l'amplificador té un comportament de dos pols, les dues constants de temps són més complicades del que l'expressió anterior suggereix perquè la capacitat de Miller no té una freqüència de dependència baixa a buri. freqüències, però té un efecte considerable a freqüències altes. És a dir, suposant que el producte RC de sortida, C_L(R_o||R_L), correspon a una freqüència molt per sobre del pol de baixa freqüència, s'ha d'utilitzar la forma precisa de la capacitat de Miller, en lloc de l'aproximació de Miller. Segons l'article sobre l'efecte Miller, la capacitat de Miller ve donada per

$\begin{array}{cc}{C}_M& =C_C(1-\frac{v_{\ell }}{v_i})\\ & =C_C(1-A_v\frac{R_L}{R_L+R_o}\frac{1+j\omega C_C{R}_o/A_v}{1+j\omega (C_L+C_C)(R_o\Vert R_L)}).\\ \end{array}$

(Per a una capacitat de Miller positiva, A _v és negativa.) En substituir aquest resultat per l'expressió de guany i els termes de recollida, el guany es reescriu com:

$\frac{v_{\ell }}{v_a}=A_v\frac{R_i}{R_i+R_A}\frac{R_L}{R_L+R_o}\frac{1+j\omega C_C{R}_o/A_v}{D_{\omega }}$

amb D _ω donat per una quadràtica en ω, és a dir:

$D_{\omega }$ $=[1+j\omega (C_L+C_C)(R_o\Vert R_L)]$ $\cdot [1+j\omega C_i(R_A\Vert R_i)]$ $+j\omega C_C(R_A\Vert R_i)$ $\cdot (1-A_v\frac{R_L}{R_L+R_O})$ $+(j\omega {)}^2{C}_C{C}_L(R_A\Vert R_i)(R_O\Vert R_L).$

Cada quadrat té dos factors, i aquesta expressió sembla més senzilla si es reescriu com

$D_{\omega }=(1+j\omega {\tau }_1)(1+j\omega {\tau }_2)$

$=1+j\omega ({\tau }_1+{\tau }_2))+(j\omega {)}^2{\tau }_1{\tau }_2$

on ${\tau }_1$ i ${\tau }_2$ són combinacions de les capacitats i resistències de la fórmula de D_ω. Corresponen a les constants de temps dels dos pols de l'amplificador. Una o altra constant de temps és la més llarga; suposar ${\tau }_1$ és la constant de temps més llarga, corresponent al pol més baix, i suposem ${\tau }_1$ >> ${\tau }_2$. (La resposta a un bon pas requereix ${\tau }_1$ >> ${\tau }_2$. Vegeu la selecció de C_C a continuació).

A freqüències baixes prop del pol més baix d'aquest amplificador, normalment el terme lineal en ω és més important que el terme quadràtic, de manera que el comportament de baixa freqüència de D_ω és:

$\begin{array}{cc}{D}_{\omega }& =1+j\omega [(C_M+C_i)(R_A\Vert R_i)+(C_L+C_C)(R_o\Vert R_L)]\\ & =1+j\omega ({\tau }_1+{\tau }_2)\approx 1+j\omega {\tau }_1\\ \end{array}$

on ara C _M es redefineix utilitzant l'aproximació de Miller com

$C_M=C_C(1-A_v\frac{R_L}{R_L+R_o}),$

que és simplement la capacitat de Miller anterior avaluada a baixes freqüències. Sobre aquesta base ${\tau }_1$ està determinat, sempre ${\tau }_1$ >> ${\tau }_2$. Com que C_M és gran, la constant de temps ${\tau }_1$ és molt més gran que el seu valor original de C_i(R_A||R_i).

A altes freqüències, el terme quadràtic esdevé important. Suposant el resultat anterior per ${\tau }_1$ és vàlid, la segona constant de temps, la posició del pol d'alta freqüència, es troba a partir del terme quadràtic en D_ω com

${\tau }_2=\frac{{\tau }_1{\tau }_2}{{\tau }_1}\approx \frac{{\tau }_1{\tau }_2}{{\tau }_1+{\tau }_2}.$

Substituint en aquesta expressió el coeficient quadràtic corresponent al producte ${\tau }_1{\tau }_2$ juntament amb l'estimació per ${\tau }_1$, es troba una estimació de la posició del segon pol:

$\begin{array}{cc}{\tau }_2& =\frac{(C_C{C}_L+C_L{C}_i+C_i{C}_C)(R_A\Vert R_i)(R_O\Vert R_L)}{(C_M+C_i)(R_A\Vert R_i)+(C_L+C_C)(R_o\Vert R_L)}\\ & \approx \frac{C_C{C}_L+C_L{C}_i+C_i{C}_C}{C_M}(R_O\Vert R_L)\\ \end{array}$

i com que C_M és gran, sembla ${\tau }_2$ es redueix de mida respecte al seu valor original C_L(R_o||R_L); és a dir, el pol superior s'ha mogut encara més en freqüència a causa de C_C.

En resum, la introducció del condensador C_C va moure el pol baix més baix i el pol alt més alt, de manera que el terme divisió del pol sembla una bona descripció.

Selecció de C_C

Figura 3: diagrama de Bode idealitzat per a un disseny d'amplificador de dos pols. El guany baixa des del primer pol a f ₁ a 20 dB / dècada fins al segon pol a f ₂ on el pendent augmenta fins a 40 dB / dècada.

Quin valor és una bona opció per a C _C ? Per a un ús general, el disseny tradicional (sovint anomenat compensació de pol dominant o d'un sol pol) requereix que el guany de l'amplificador caigui a 20. dB/dècada des de la freqüència de la cantonada fins a 0 guany dB, o fins i tot inferior. Amb aquest disseny, l'amplificador és estable i té una resposta a l'esglaó gairebé òptima fins i tot com a buffer de tensió de guany unitari. Una tècnica més agressiva és la compensació bipolar.

La forma de posicionar f ₂ per obtenir el disseny es mostra a la figura 3. Al pol més baix f ₁, la trama de guany de Bode trenca el pendent per caure a 20 dB/dècada. L'objectiu és mantenir el 20 Pendent dB/dècada fins a zero dB, i prenent la relació entre la caiguda desitjada del guany (en dB) de 20 log ₁₀ A _v al canvi requerit de freqüència (en una escala de freqüència logarítmica) de (log₁₀ f₂ − log₁₀ f₁) = log ₁₀ ( f₂/f₁) el pendent del segment entre f₁ i f₂ és:

Pendent per dècada de freqüència $=20\frac{\mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{1}\mathrm{0}}(A_v)}{\mathrm{l}\mathrm{o}{\mathrm{g}}_{\mathrm{1}\mathrm{0}}(f_2/f_1)},$

que és 20 dB/dècada sempre que f₂ = A_v f₁. Si f₂ no és tan gran, la segona ruptura de la gràfica de Bode que es produeix al segon pol interromp la gràfica abans que el guany baixi a 0. dB amb la consegüent menor estabilitat i resposta de pas degradada.

La figura 3 mostra que per obtenir la dependència correcta del guany de la freqüència, el segon pol és almenys un factor A _v superior en freqüència que el primer pol. El guany es redueix una mica pels divisors de tensió a l'entrada i la sortida de l'amplificador, de manera que amb correccions a A _v per als divisors de tensió a l'entrada i la sortida, la condició de relació de pols per a una bona resposta de pas es converteix en:

$\frac{{\tau }_1}{{\tau }_2}\approx A_v\frac{R_i}{R_i+R_A}\cdot \frac{R_L}{R_L+R_o}$

Figura 4: Capacitat de Miller a baixes freqüències C _M (superior) i condensador de compensació C _C (inferior) en funció del guany mitjançant Excel. Les unitats de capacitat són pF.

Utilitzant les aproximacions de les constants de temps desenvolupades anteriorment,

$\frac{{\tau }_1}{{\tau }_2}\approx \frac{({\tau }_1+{\tau }_2{)}^2}{{\tau }_1{\tau }_2}\approx A_v\frac{R_i}{R_i+R_A}\cdot \frac{R_L}{R_L+R_o},$

$\frac{[(C_M+C_i)(R_A\Vert R_i)+(C_L+C_C)(R_o\Vert R_L){]}^2}{(C_C{C}_L+C_L{C}_i+C_i{C}_C)(R_A\Vert R_i)(R_O\Vert R_L)}$ $\cdot =A_v\frac{R_i}{R_i+R_A}\cdot \frac{R_L}{R_L+R_o},$

que proporciona una equació quadràtica per determinar un valor adequat per a C_C. La figura 4 mostra un exemple amb aquesta equació. Amb valors baixos de guany, aquest exemple d'amplificador satisfà la condició de relació de pols sense compensació (és a dir, a la figura 4, el condensador de compensació C_C és petit amb guany baix), però a mesura que augmenta el guany, es fa necessària ràpidament una capacitat de compensació (és a dir, a la figura 4, el condensador de compensació C_C augmenta ràpidament amb el guany) perquè la proporció de pols necessària augmenta amb el guany. Per a un guany encara més gran, el C_C necessari disminueix amb l'augment del guany perquè l'amplificació de Miller de C _C, que augmenta amb el guany (vegeu l'equació de Miller), permet un valor més petit per a C_C.

Per proporcionar més marge de seguretat per a les incerteses de disseny, sovint A _v s'augmenta a dues o tres vegades A _v al costat dret d'aquesta equació. Vegeu Sansen o Huijsing i l' article sobre la resposta a l'esglaó.