Fitxer:Lemniscates5.png

Aquest fitxer prové de Wikimedia Commons i pot ser usat per altres projectes. La descripció de la seva pàgina de descripció es mostra a continuació.

|
Aquesta imatge (de tipus gràfic) s'hauria de tornar a crear utilitzant gràfics vectorials com ara un fitxer SVG. Això té diversos avantatges; en trobareu més informació a Commons:Media for cleanup. Si ja disposeu d'una versió d'aquesta imatge en format SVG, us preguem que la pengeu; després, reemplaceu aquesta plantilla amb la plantilla {{Vector version available|nom nou de la imatge.svg}} en aquesta imatge.
|
Resum
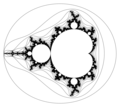
| DescripcióLemniscates5.png | 6 lemniscates of Mandelbrot set. Computed using implicit equations. |
| Font | self-made with help of many people, using free CAS Maxima, Gnuplot and implicit_plot package (by Andrej Vodopivec) |
| Autor | Adam majewski |
| Altres versions | lemniscates for Julia set |
Compare with
-
DEM and sobel
-
LCM/J; ER=1000
-
LCM/J but better algorithm, ER = 2
-
LSM/J B&W; ER = 1000
-
LSM/J colour ( probably made with Fractint ); ER = 2
See also:
Long description
" instead of iterating a point through a nice fractal-generating function until it exits the containing circle, I'm starting with the containing circle's function (2cos(t),2sin(t)) and iterating that circle function through the inverse of the fractal-generating function." Axis Angels[1]
Few lemniscates of Mandelbrot set[2]. They are boundaries of Level Sets of escape time ( LSM/M [3]).
They are in parameter plane (c-plane, complex plane ).
Definition :

where








One can compute first few iterations :



and so on .
Then :



...


These curves tend to boundary of Mandelbrot set as n goes to infinity.
If ER < 2 they are inside Mandelbrot set[6].
If ER = 2 curves meet together ( have common point) c = −2. Thus they can't be equipotential lines.
If ER ≥ 2 they are outside of Mandelbrot set. They can also be drawn using Level Curves Method.
If ER >> 2 they aproximate equipotential lines ( level curves of real potential , see CPM/M ).
Maxima source code
/* based on the code by Jaime Villate */ load(implicit_plot); /* package by Andrej Vodopivec */ c: x+%i*y; ER:2; /* Escape Radius = bailout value it should be >=2 */ f[n](c) := if n=1 then c else (f[n-1](c)^2 + c); ip_grid:[100,100]; /* sets the grid for the first sampling in implicit plots. Default value: [50, 50] */ ip_grid_in:[15,15]; /* sets the grid for the second sampling in implicit plots. Default value: [5, 5] */ my_preamble: "set zeroaxis; set title 'Boundaries of level sets of escape time of Mandelbrot set'; set xlabel 'Re(c)'; set ylabel 'Im(c)'"; implicit_plot(makelist(abs(ev(f[n](c)))=ER,n,1,6), [x,-2.5,2.5],[y,-2.5,2.5],[gnuplot_preamble, my_preamble], [gnuplot_term,"png size 1000,1000"],[gnuplot_out_file, "lemniscates6.png"]);
For curves 1-5 it works, but for curve number 6 this program fails( also Mathematica program[7]), because of floating point error.
One have to change the method of computing lemniscates . Here is the code and explanation by Andrej Vodopivec" "You can trick implicit_plot to do computations in higher precision. Implicit_draw will draw the boundary of the region where the function has negative value. You can define a function f6 which computes the sign of f[6] using bigfloats and then plot f6."
/* based on the code by Jaime Villate and Andrej Vodopivec*/ c: x+%i*y; ER:2; f[n](c) := if n=1 then c else (f[n-1](c)^2 + c); F(x,y):=block([x:bfloat(x), y:bfloat(y)],if abs((f[6](c)))>ER then 1 else -1); fpprec:32; load(implicit_plot); /* package by Andrej Vodopivec */ ip_grid:[100,100]; ip_grid_in:[15,15]; implicit_plot(append(makelist(abs(ev(f[n](c)))=ER,n,1,5), ['(F(x,y))]),[x,-2.5,2.5],[y,-2.5,2.5]);
Questions
- What is mathemathical description of these curves ?
Rerferences
- ↑ You tube video
- ↑ lemniscates at Mandelbrot Set Glossary and Encyclopedia, by Robert Munafo
- ↑ LSM/M
- ↑ Weisstein, Eric W. "Pear Curve." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PearCurve.html
- ↑ Mandelbrot lemniscate at 2DCurves by Jan Wassenaar
- ↑ Polynomial_lemniscate
- ↑ | Weisstein, Eric W. "Mandelbrot Set Lemniscate." From MathWorld--A Wolfram Web Resource.
Llicència

|
S'autoritza la còpia, la distribució i la modificació d'aquest document sota els termes de la llicència de documentació lliure GNU versió 1.2 o qualsevol altra versió posterior que publiqui la Free Software Foundation; sense seccions invariants, ni textos de portada, ni textos de contraportada. S'inclou una còpia d'aquesta llicència en la secció titulada GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
- Sou lliure de:
- compartir – copiar, distribuir i comunicar públicament l'obra
- adaptar – fer-ne obres derivades
- Amb les condicions següents:
- reconeixement – Heu de donar la informació adequada sobre l'autor, proporcionar un enllaç a la llicència i indicar si s'han realitzat canvis. Podeu fer-ho amb qualsevol mitjà raonable, però de cap manera no suggereixi que l'autor us dóna suport o aprova l'ús que en feu.
- compartir igual – Si modifiqueu, transformeu, o creeu a partir del material, heu de distribuir les vostres contribucions sota una llicència similar o una de compatible amb l'original.
Llegendes
Elements representats en aquest fitxer
representa l'entitat
Algun valor sense element de Wikidata
Historial del fitxer
Cliqueu una data/hora per veure el fitxer tal com era aleshores.
| Data/hora | Miniatura | Dimensions | Usuari/a | Comentari | |
|---|---|---|---|---|---|
| actual | 20:42, 11 gen 2009 |  | 1.000 × 1.000 (73 Ko) | wikimediacommons>Geek3 | smooth and precise plotcurve |
Ús del fitxer
La pàgina següent utilitza aquest fitxer: