Superfície de Catalan

Una superfície de Catalan.

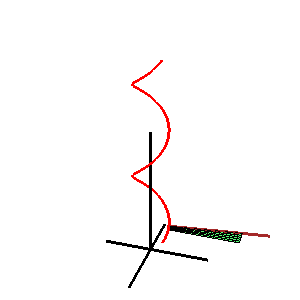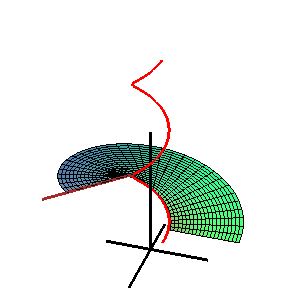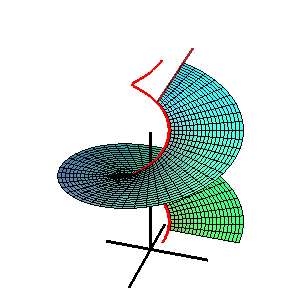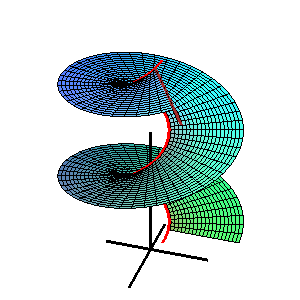
En geometria, una superfície de Catalan, anomenada així pel matemàtic belga Eugène Charles Catalan, és una superfície reglada on tots els regles són paral·lels a un pla fix.

Equacions

L'equació vectorial d'una superfície de Catalan ve donada per

r = s(u) + v L(u),

On r = s(u) és la corba espacial i L(u) és el vector unitari del regle a u = u. Tots els vectors L(u) són paral·lels al mateix pla, anomenat pla directriu de la superfície. Això pot ser caracteritzat per la condició: producte mixt [L(u), L' (u), L" (u)] = 0.[1]

Les equacions paramètriques de la superfície de Catalan són [2]

$x=f(u)+vi(u),y=g(u)+vj(u),z=h(u)+vk(u)$

Casos especials

Si tot els regles d'una superfície de Catalan interseccionen una recta fixa, llavors la superfície és anomenada un conoide.

Catalan va provar que l'helicoide i el pla eren les úniques superfícies mínimes reglades.

Referències

• A. Gray, E. Abbena, S. Salamon, Modern differential geometry of curves and surfaces with Mathematica, 3rd ed. Boca Raton, Florida:CRC Press, 2006. [3] (Plantilla:ISBN)
• Plantilla:Springer
• V. Y. Rovenskii, Geometry of curves and surfaces with MAPLE [4] (Plantilla:ISBN)