Estrofoide

Construcció de lPlantilla:'Estrofoide dreta de pol X i de punt fix O, prenent per corba base l'eix Oy.

En matemàtiques, i més precisament en geometria, una corba estrofoide, o simplement una estrofoide, és una corba engendrada a partir d'una corba donada C i de dos punts A (el punt fix) i O (el pol).

En el cas particular on C és una recta, A pertany a C, i O no pertany a C, la corba s'anomena una estrofoide obliqua. Si, de més OA és perpendicular a C, la corba és anomenada una estrofoide dreta, o simplement una estrofoide per certs autors. L'estrofoide dreta de vegades també s'anomena corba logocíclica.

Construcció

Construcció d'una estrofoide en el cas general

La corba Estrofoidal que correspon a la corba C, amb el punt fix A i el pol O es construeix de la manera següent: sigui L una recta mòbil que passa per O i que talla C en K. Siguin llavors P₁ i P₂ els dos punts de L tals que P₁K = P₂K = AK. El lloc geomètric dels punts P ₁ i P₂ s'anomena l'estrofoide de C relativa al pol O i amb el punt fix A. S'observa que AP₁ i AP₂ són ortogonals.

Equacions

Coordenades polars

Sigui la corba C donada per $r=f(\theta )$, on l'origen es pren a O. Sigui A el punt de coordenades cartesianes (a, b). Si $K=(r\cos \theta ,r\sin \theta )$ és un punt de la corba, la distància de K à A és

$d=\sqrt{(r\cos \theta -a{)}^2+(r\sin \theta -b{)}^2}=\sqrt{(f(\theta )\cos \theta -a{)}^2+(f(\theta )\sin \theta -b{)}^2}$.

Els punts de la recta OK tenen per angle polar $\theta$, i els punts a distància d de K sobre aquesta recta són a una distància $f(\theta )\pm d$ de l'origen. Per tant, l'equació de l'estrofoide ve donada per

$r=f(\theta )\pm \sqrt{(f(\theta )\cos \theta -a{)}^2+(f(\theta )\sin \theta -b{)}^2}$.

Coordenades cartesianes

Sigui C d'equacions paramètriques (x=x (t),y =y(t)). Sigui A el punt (a, b) i O el punt (p, q). Llavors, les fórmules polars precedents mostren que la representació paramètrica de l'estrofoide és:

$x=u(t)=p+(x(t)-p)(1\pm n(t)),y=v(t)=q+(y(t)-q)(1\pm n(t))$,

on

$n(t)=\sqrt{\frac{(x(t)-a{)}^2+(y(t)-b{)}^2}{(x(t)-p{)}^2+(y(t)-q{)}^2}}$.

Una altra fórmula polar

La complexitat de les fórmules precedents limita la seva utilitat a la pràctica. Existeix per això una forma alternativa de vegades més senzilla, que és particularment útil quan C és una sectriu de Maclaurin de pols O i A.

Sigui O l'origen i A el punt (a, 0). Sigui K un punt de la corba, $\theta$ l'angle entre OK i l'eix OX, i $\vartheta$ l'angle entre AK i l'eix OX. Se suposa que $\vartheta$ es doni en funció de $\theta$, sota la forma $\vartheta =l(\theta )$. Sigui $\psi$ l'angle en K, dons $\psi =\vartheta -\theta$. Es pot determinar r en funció de l fent servir la llei del sinus: com

$\frac{r}{\sin \vartheta }=\frac{a}{\sin \psi },r=a\frac{\sin \vartheta }{\sin \psi }=a\frac{\sin l(\theta )}{\sin (l(\theta )-\theta )}$.

Siguin P₁ i P₂ els punts de la recta OK a distància AK de K, numerats de forma que $\psi =\widehat{P_{1}Ka}$ i $\pi -\psi =\widehat{Ak{p}_2}$. El triangle $P_{1}KA$ és isòsceles d'angle al vèrtex $\psi$, per tant els angles de la base, $\widehat{A{P}_{1}K}$ i $\widehat{KA{P}_1}$, valent$(\pi -\psi )/2$. L'angle entre AP ₁ i l'eix OX és llavors

$l_1(\theta )=\vartheta +\mathrm{\angle }KA{P}_1=\vartheta +(\pi -\psi )/2=\vartheta +(\pi -\vartheta +\theta )/2=(\vartheta +\theta +\pi )/2$.

Emprant el fet que AP₁ i AP₂ són perpendiculars (ja que el triangleAP₁P₂ és inscrit en un semicercle), l'angle entre Ap₂ i l'eix OX val

$l_2(\theta )=(\vartheta +\theta )/2$.

L'equació polar de l'estrofoide es dedueix llavors de l ₁ i l₂ segons les fórmules precedents:

$r_1=a\frac{\sin l_1(\theta )}{\sin (l_1(\theta )-\theta )}=a\frac{\sin ((l(\theta )+\theta +\pi )/2)}{\sin ((l(\theta )+\theta +\pi )/2-\theta )}=a\frac{\cos ((l(\theta )+\theta )/2)}{\cos ((l(\theta )-\theta )/2)}$

$r_2=a\frac{\sin l_2(\theta )}{\sin (l_2(\theta )-\theta )}=a\frac{\sin ((l(\theta )+\theta )/2)}{\sin ((l(\theta )+\theta )/2-\theta )}=a\frac{\sin ((l(\theta )+\theta )/2)}{\sin ((l(\theta )-\theta )/2)}$

C és una sectriu de Maclaurin de pols O i A quan l és de la forma $q\theta +{\theta }_0$; en aquest cas l₁ i l₂ tenen la mateixa forma, i l'estrofoide és o bé una altra sectriu de Maclaurin, o bé una parella de sectrius; se'n pot trobar una equació polar senzilla si es pren l'origen al punt simètric de A respecte de O.

Casos particulars

Estrofoides obliqües

Soit C une droite passant par A. Alors, dans les notations précédentes, $l(\theta )=\alpha$, où$\alpha$ est une constante, et $l_1(\theta )=(\theta +\alpha +\pi )/2$; $l_2(\theta )=(\theta +\alpha )/2$. Avec l'origine en O, les équations polaires de la estrofoide correspondante, appelée une estrofoide oblique deviennent

Sigui C una recta que passa per A. Llavors, en les notacions precedents, $l(\theta )=\alpha$, on $\alpha$ és una constant, i $l_1(\theta )=(\theta +\alpha +\pi )/2$; $l_2(\theta )=(\theta +\alpha )/2$. Amb l'origen a O, les equacions polars de l'estrofoide corresponent, anomenada una estrofoide obliqua esdevenen

$r=a\frac{\cos ((\alpha +\theta )/2)}{\cos ((\alpha -\theta )/2)}$

i

$r=a\frac{\sin ((\alpha +\theta )/2)}{\sin ((\alpha -\theta )/2)}$.

Es verifica fàcilment que aquestes dues equacions descriuen de fet la mateixa corba.

Desplaçant l'origen en A (veure, l'article sectriu de Maclaurin) i reemplaçant −a per a, s'obté

$r=a\frac{\sin (2\theta -\alpha )}{\sin (\theta -\alpha )}$ ;

una rotació de $\alpha$ transforma aquesta equació en

$r=a\frac{\sin (2\theta +\alpha )}{\sin (\theta )}$.

En coordenades cartesianes (i canviant les constants), s'obté

$y(x^2+y^2)=b(x^2-y^2)+2cxy$.

És una cúbica, unicursal segons l'equació polar. Posseeix una sungularitat a (0, 0), i la recta y =b n'és asímptota.

L'estrofoide dreta

Estrofoide dreta.

Posant $\alpha =\pi /2$ en

$r=a\frac{\sin (2\theta -\alpha )}{\sin (\theta -\alpha )}$,

s'obté

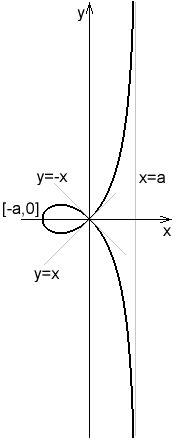
$r=a\frac{\cos 2\theta }{\cos \theta }=a(2\cos \theta -\sec \theta )$.

Aquesta corba s'anomena lPlantilla:'estrofoide dreta, i correspon al cas on C és l'eix Oy, O és l'origen, i A és el punt (a,0).

L'equació cartesiana és

$y^2=x^2(a-x)/(a+x)$;

una representació paramètrica unicursal és:

$x=-a\frac{1-t^2}{1+t^2}$

$y=-at\frac{1-t^2}{1+t^2}$.

La corba s'assembla al foli de Descartes, i la recta x = −a és asímptota en les dues branques infinites. La corba posseeix dues asímptotes més "imaginaries" en el pla complex ${ℂ}^2$, donades per

$x\pm iy=-a$.

Estrofoides de circumferències que pasen pels punts fixos

Sigui C una circumferència que passa per O i A. Prenent O per origen i A en (a, 0), s'obté, amb les notacions precedents, $l(\theta )=\alpha +\theta$, on $\alpha$ és una constant. Així, $l_1(\theta )=\theta +(\alpha +\pi )/2$ i $l_2(\theta )=\theta +\alpha /2$. Llavors les equacions polars de les estrofoides corresponents són

$r=a\frac{\cos (\theta +\alpha /2)}{\cos (\alpha /2)}$

i

$r=a\frac{\sin (\theta +\alpha /2)}{\sin (\alpha /2)}$.

Són les equacions de dos circumferències que passen també per O i A, i formen angles de $\pi /4$ amb C en aquests punts.

Referències

• Al lloc web de Robert Ferreol, a la seva enciclopèdia de les formes matemàtiques destacables:
  • "Courbe Strophoïdale"
  • "estrofoide"
  • "estrofoide Droite", on també es troben moltes propietats geomètriques d'aquesta corba.

• Al lloc web de Mathworld
  • Plantilla:MathWorld
  • Plantilla:MathWorld