Funció d'activació

Esquema de blocs d'un perceptró: entrades, suma d'entrades, funció d'Activació i sortida

Funció d'Activació Lògica

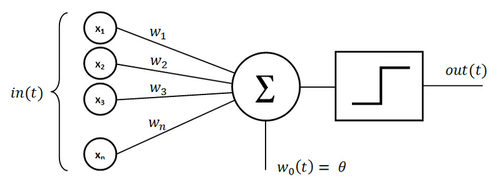
A les xarxes neuronals artificials, la funció d'activació d'un node defineix la sortida d'aquest node donada una entrada o un conjunt d'entrades. Un circuit integrat estàndard es pot veure com una xarxa digital de funcions d'activació que pot ser "ON" (1) o "OFF" (0), segons l'entrada. Això és similar al perceptró lineal de les xarxes neuronals. Tanmateix, només les funcions d'activació no lineals permeten que aquestes xarxes calculin problemes no trivials utilitzant només un nombre reduït de nodes, i aquestes funcions d'activació s'anomenen no linealitats.

Les funcions d'activació més habituals es poden dividir en tres categories: funcions de cresta, funcions radials i funcions de plec.

La taula següent compara les propietats de diverses funcions d'activació més usuals :

Nom	Gràfic	Equació	Derivada	Validesa	Ordre de continuïtat	Derivable
Identitat/Rampa		$f(x)=x$	$f^{\prime }(x)=1$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^{\mathrm{\infty }}$	Sí
Esglaó/Heaviside		$f(x)=\{\begin{array}{ccc}0& \text{si}& x<0\\ 1& \text{si}& x\ge 0\end{array}$	$f^{\prime }(x)=\{\begin{array}{ccc}0& \text{si}& x\ne 0\\ ?& \text{si}& x=0\end{array}$	$\{0,1\}$	$C^{-1}$	NO
Lògica (o esglaó suau, o sigmoide)		$f(x)=\frac{1}{1+{\mathrm{e}}^{-x}}$	$f^{\prime }(x)=f(x)(1-f(x))$	$(0,1)$	$C^{\mathrm{\infty }}$	Sí
Tangent hiperbòlica		$f(x)=\tanh (x)=\frac{2}{1+{\mathrm{e}}^{-2x}}-1$	$f^{\prime }(x)=1-f(x{)}^2$	$(-1,1)$	$C^{\mathrm{\infty }}$	Sí
Arc tangent		$f(x)={\tan }^{-1}(x)$	$f^{\prime }(x)=\frac{1}{x^2+1}$	$(-\frac{\pi }{2},\frac{\pi }{2})$	$C^{\mathrm{\infty }}$	Sí
Signe suau		$f(x)=\frac{x}{1+|x|}$	$f^{\prime }(x)=\frac{1}{(1+|x|{)}^2}$	$(-1,1)$	$C^1$	Sí
Unitat de rectifició lineal (ReLU)		$f(x)=\{\begin{array}{ccc}0& \text{si}& x<0\\ x& \text{si}& x\ge 0\end{array}$	$f^{\prime }(x)=\{\begin{array}{ccc}0& \text{si}& x<0\\ 1& \text{si}& x\ge 0\end{array}$	$[0,\mathrm{\infty }[$	$C^0$	Sí
Unitat de rectificació lineal paramètric (PReLU)		$f(x)=\{\begin{array}{ccc}\alpha x& \text{si}& x<0\\ x& \text{si}& x\ge 0\end{array}$	$f^{\prime }(x)=\{\begin{array}{ccc}\alpha & \text{si}& x<0\\ 1& \text{si}& x\ge 0\end{array}$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^0$	Sí
Unitat exponencial lineal (ELU)		$f(x)=\{\begin{array}{ccc}\alpha ({\mathrm{e}}^x-1)& \text{si}& x<0\\ x& \text{si}& x\ge 0\end{array}$	$f^{\prime }(x)=\{\begin{array}{ccc}f(x)+\alpha & \text{si}& x<0\\ 1& \text{si}& x\ge 0\end{array}$	$(-\alpha ,\mathrm{\infty })$	$C^1$ si $\alpha =1$	Sí
Unitat de rectificació lineal suau (SoftPlus)		$f(x)=\ln (1+{\mathrm{e}}^x)$	$f^{\prime }(x)=\frac{1}{1+{\mathrm{e}}^{-x}}$	$(0,\mathrm{\infty })$	$C^{\mathrm{\infty }}$	Sí
Identitat corba		$f(x)=\frac{\sqrt{x^2+1}-1}{2}+x$	$f^{\prime }(x)=\frac{x}{2\sqrt{x^2+1}}+1$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^{\mathrm{\infty }}$	Sí
Exponencial suau paramètrica (Plantilla:Lang)		$f(\alpha ,x)=\{\begin{array}{ccc}-\frac{\ln (1-\alpha (x+\alpha ))}{\alpha }& \text{si}& \alpha <0\\ x& \text{si}& \alpha =0\\ \frac{{\mathrm{e}}^{\alpha x}-1}{\alpha }+\alpha & \text{si}& \alpha >0\end{array}$	$f^{\prime }(\alpha ,x)=\{\begin{array}{ccc}\frac{1}{1-\alpha (\alpha +x)}& \text{si}& \alpha <0\\ {\mathrm{e}}^{\alpha x}& \text{si}& \alpha \ge 0\end{array}$	$(-\mathrm{\infty },\mathrm{\infty })$	$C^{\mathrm{\infty }}$	Sí
Sinusoide		$f(x)=\sin (x)$	$f^{\prime }(x)=\cos (x)$	$[-1,1]$	$C^{\mathrm{\infty }}$	Sí
Sinus cardinal		$f(x)=\{\begin{array}{ccc}1& \text{si}& x=0\\ \frac{\sin (x)}{x}& \text{si}& x\ne 0\end{array}$	$f^{\prime }(x)=\{\begin{array}{ccc}0& \text{si}& x=0\\ \frac{\cos (x)}{x}-\frac{\sin (x)}{x^2}& \text{si}& x\ne 0\end{array}$	$[\approx -.217234,1]$	$C^{\mathrm{\infty }}$	Sí
Funció gaussienne		$f(x)={\mathrm{e}}^{-x^2}$	$f^{\prime }(x)=-2x{\mathrm{e}}^{-x^2}$	$]0,1]$	$C^{\mathrm{\infty }}$	Sí