Funció contínua

Plantilla:Falten referències Plantilla:Redirecció Funció contínua és un terme utilitzat en matemàtiques i, en particular, en topologia.

Definició matemàtica per funcions de variables reals

Funció contínua en un punt

Siguin $I$ un interval de $ℝ$, $f$ una aplicació de $I$ a $ℝ$, i $x_0$ un punt de $I$.

1. Si $x_0\in I$ i $x_0$ és un punt d'acumulació de $I$, direm que $f$ és contínua en el punt $x_0$ si $\underset{x\to x_0}{\lim }f(x)=f(x_0)$.
2. Si $x_0\in I$ i $x_0$ no és un punt d'acumulació de $I$, direm que $f$ és contínua per definició.

La definició anterior també es pot formular en termes de distàncies, diem que $f$ és contínua en el punt $x_0$ del seu domini si i només si:

$\mathrm{\forall }\epsilon >0,\mathrm{\exists }\delta >0,x\in ]x_0-\delta ,x_0+\delta [\cap I⟹|f(x)-f(x_0)|\le \epsilon$

És a dir, una funció és contínua quan per qualsevol punt $x$ del seu domini podem trobar un interval tal que la seva imatge estigui continguda en un interval tan petit com vulguem al voltant de la seva imatge $f(x)$.

Finalment, en termes de successions tenim la següent propietat: La funció $f$ és contínua en el punt $x_0\in I$ si i només si per qualsevol successió $\{x_n\}\subset I$ $$\{x_n\}\to x_0⟹\{f(x_n)\}\to f(x_0).$$Aquesta propietat s'anomena continuïtat seqüencial de $f$ en el punt $x_0$.

Continuïtat per la dreta i per l'esquerra

Suposem que la funció $f$ està definida en l'interval tancat $[a,b]$ i sigui $x_0\in [a,b[$. Es diu que el nombre $\ell$ és el límit per la dreta de $f$ en $x_0$ si $\mathrm{\forall }\epsilon >0,\mathrm{\exists }\delta >0$ tal que si $x\in ]a,b[$ compleix que $0<x-x_0<\delta$ (és dir, $x$ està a la dreta de $x_0$), aleshores $|f(x)-\ell |<\epsilon$; en aquest cas, s'escriu $\ell =f(x_0^{+})$ i s'utilitza la notació $$\underset{x\to x_0^{+}}{\lim }f(x)=f(x_0^{+})\text{o}\underset{x\downarrow x_0}{\lim }f(x)=f(x_0^{+}).$$Es diu que $f$ és continua per la dreta en el punt $x_0$ si $f(x_0^{+})=f(x_0)$ .

De manera anàloga, per a $x_0\in ]a,b]$ es defineix el límit per l'esquerra de $f$ en el punt $x_0$ i s'escriu

$$\underset{x\to x_0^{-}}{\lim }f(x)=f(x_0^{-})\text{o}\underset{x\uparrow x_0}{\lim }f(x)=f(x_0^{-}).$$

Es diu que $f$ és continua per l'esquerra en el punt $x_0$ si $f(x_0^{-})=f(x_0)$.

Propietat. Sigui $x_0\in ]a,b[$. Aleshores $f$ és contínua en el punt $x_0$ si i només si $f(x_0)=f(x_0^{+})=f(x_0^{-})$.

Vegeu més avall la secció discontinuïtats de salt per un exemple de funció on el límit per la dreta i per l'esquerra en un punt no coincideixen.

Continuïtat en un interval

Sigui $[a,b]$ un subconjunt del domini d'una funció $f$. Es diu que $f$ és contínua en $[a,b]$ (en llenguatge matemàtic, $f\in {𝒞}^0[a,b]$) si és contínua en tots el punts d'aquest interval.

És a dir:

$\mathrm{\forall }x\in [a,b],\mathrm{\forall }\epsilon >0,\mathrm{\exists }\delta >0,y\in ]x-\delta ,x+\delta [\cap I⟹|f(x)-f(y)|\le \epsilon$

que equival a què:

• $f$ és contínua a $(a,b)$ (en llenguatge matemàtic, $f\in {𝒞}^0(a,b)$).
• En els extrems de l'interval es compleix $f(a)=f(a^{+})$ i $f(b)=f(b^{-})$

Evidentment, en la definició el número $\delta$ depèn de $ϵ$, ja que si $ϵ$ es fa més petit, pot ser que hàgim de buscar un $\delta$ més petit. Però en aquest apartat cal aclarir que el número $\delta$ també depèn del punt $x$, és a dir, per un mateix valor de $ϵ$, un valor de $\delta$ que serveix per algun punt en concret pot no servir per un altre punt. En general, donat un valor de $ϵ$ no existeix un valor de $\delta$ que serveixi per a tots els punts $x\in [a,b]$, tot i així, quan aquest valor existeix parlem de continuïtat uniforme.

Derivabilitat i continuïtat

Qualsevol funció derivable en un punt o en un interval, és igualment contínua en aquest punt o interval.

El recíproc és fals.

Per exemple, la funció $f(x)=|x|$ (valor absolut de $x$ és una funció contínua a $ℝ$, en canvi, no és derivable en el punt $x=0$.

Funcions usuals

Les funcions polinòmiques, exponencials, logarítmiques, hiperbòliques, trigonomètriques són derivables en els intervals en què estan definides, i són, doncs, igualment contínues en aquests intervals.

Teoremes sobre funcions contínues

Teorema dels compactes

"

$f$

contínua en un Plantilla:Subratllat

$K⟹f(K)$

és compacte."

Efectivament, per demostrar que

$f(K)$

és un compacte necessitem veure que, sigui

$y_a=f(x_a),\mathrm{\forall }{x}_a\in K$

, la successió

$\{y_a\}$

té alguna successió parcial convergent

$\{y_{a_i}\}$

.

Com que, per hipòtesi $K$ és un compacte, existeix alguna successió parcial $\{x_{a_i}\}$ convergent. Sigui $l$ el límit d'aquesta successió $(\{x_{a_i}\}\to l)$, per la definició de continuïtat (definició per successions) tenim que $\{f(x_{a_i})\}\to f(l)\in f(K)$. Però per la definició que hem fet al principi, $\{f(x_{a_i})\}=\{y_{a_i}\}\to f(l)$ resultant així que $\{y_{a_i}\}$ (que és una successió parcial de $\{y_a\}$) és convergent. I $f(K)$ és un compacte.

Teorema del màxim i el mínim

"

$f$

contínua en un Plantilla:Subratllat

$K⟹f(K)$

té màxim i mínim."

Efectivament, pel teorema dels compactes si

$f$

és contínua en el compacte

$K$

,

$f(K)$

és compacte. Com que qualsevol compacte és fitat, existiran un suprem (

$s$

) i un ínfim (

$i$

). Demostrem ara que

$s,i\in K$

. En efecte, podem trobar valors tan a prop de

$s$

com vulguem (si no fos així, podríem trobar una fita superior més petita que

$s$

, arribant a una contradicció), per tant podem construir una successió

$\{s_n\}$

que convergeixi a

$s$

. Com que

$f(K)$

és un compacte

$f(K)$

és tancat i per tant,

$s\in f(K)$

. Sent

$s$

el màxim del compacte

$f(K)$

.

$f(c)<0$

De manera anàloga podem trobar valors tan a prop de $i$ com vulguem (o arribem a una contradicció), per tant, podem construir una successió $\{i_n\}\to i$. I com que $f(K)$ és tancat $i\in f(K)$, sent el mínim d'aquest compacte.

Teorema de Bolzano

"

$f\in {𝒞}^0[a,b]$

amb

$f(a)\cdot f(b)<0$

(és a dir, no nuls i de signe oposat)

$⟹\mathrm{\exists }c\in (a,b)$

on

$f(c)=0$

."

Efectivament, anomenem

$I_0=[a,b]$

, sigui

$c_0$

el punt central d'aquest interval. Si

$f(c_0)=0$

el teorema queda demostrat. Si

$f(c_0)\ne 0$

, aleshores partim l'interval

$I_0$

en els intervals

$[a,c_0]$

i

$[c_0,b]$

. Com que

$f(a)$

i

$f(b)$

tenen signes oposats,

$f(c_0)$

tindrà el mateix signe que un dels dos i tindrà signe oposat que l'altre. Anomenem

$I_1$

a l'interval en que

$f$

tingui signes oposats en els extrems, i definim

$c_1$

com el punt central de

$I_1$

. De nou repetim el mateix procés, si

$f(c_1)=0$

hem acabat, si no, definim

$I_2,I_3,...$

Si per algun interval

$I_i$

es compleix que

$f(c_i)=0$

hem acabat, si no tenim definits infinits intervals en els quals

$f$

pren valors oposats en els extrems.

Notem que es compleix sempre que $I_0\supset I_1\supset I_2\supset ...$ i la longitud de cada interval és: $L_0=b-a,L_1=\frac{b-a}{2},L_2=\frac{b-a}{4},...,L_n=\frac{b-a}{2^n}$.

Construïm la successió $x_n\in I_n$. Sigui $I_{n_0}$ un interval de longitud $L_{n_0}=\frac{b-a}{2^{n_0}}$, aleshores és clar que $|x_n-x_m|\le \frac{b-a}{2^{n_0}},\mathrm{\forall }n,m>n_0$ ja que $I_n,I_m\subset I_{n_0}$. Per tant,$\mathrm{\forall }ϵ>0,\mathrm{\exists }{n}_0\in \mathbb{N}$ tal que $L_{n_0}=\frac{b-a}{2^{n_0}}\le ϵ$ i, en conseqüència $|x_n-x_m|\le \frac{b-a}{2^{n_0}}\le ϵ,\mathrm{\forall }m,n>n_0$. Per tant, la successió $\{x_n\}$ és una successió de Cauchy i, per tant, és convergent. Denotem $c=\lim \{x_n\}$. Suposem que $f(c)>0$, aleshores per continuïtat podem trobar un interval $I$ que compleixi que $f(x)>0$ en tot l'interval. Però a partir d'algun subíndex $I_n\subset I$ i existeix algun punt de $I_n$ en que $f(x)<0$ (recordem que $f$ pren valors de signe oposat en els seus extrems). Igualment, si $f(c)<0$ per continuïtat podem trobar un interval $I$ que compleixi que $f(x)<0$. Però a partir d'algun subíndex $I_n\subset I$ i existeix algun punt de $I_n$ en que $f(x)>0$. Per tant, l'única possibilitat és que $f(c)=0$. Quedant així demostrat el teorema.

Teorema del valor intermedi de Bolzano

"

$f\in {𝒞}^0[a,b]$

, amb

$f(a)\ne f(b)$

, i

$u$

està entre

$f(a)$

i

$f(b)⟹\mathrm{\exists }c\in (a,b)$

on

$f(c)=u$

."

Efectivament si

$u$

està entre

$f(a)$

i

$f(b)$

, aleshores

$f(a)-u$

i

$f(b)-u$

tenen signes oposats. Definim aleshores la funció

$g(x)=f(x)-u$

, com que

$f$

és contínua en l'interval

$[a,b]$

,

$g$

és contínua en el mateix interval. Hem dit que

$g(a)=f(a)-u$

i

$g(b)=f(b)-u$

tenen signes oposats, per tant, pel teorema de Bolzano, existeix un punt

$c\in (a,b)$

que compleix que

$g(c)=f(c)-u=0⟹f(c)=u$

.

Teorema de la continuïtat de la funció inversa

"

$f$

contínua i Plantilla:Subratllat en un interval

$I⟹f$

és estrictament creixent o decreixent a

$I$

i

$f^{-1}$

és contínua a

$f(I)$

."

Efectivament, si

$f$

és invertible

$f$

ha de ser injectiva. Per tant, si per a dos punts

$a,b\in I,$$a\ne b⟹f(a)\ne f(b).$

Suposem que

$f(a)>f(b)$

, aleshores,

$\mathrm{\forall }x\in (a,b),f(a)>f(x)>f(b)$

, ja que, si

$f(x)>f(a)>f(b)$

, pel teorema del valor intermedi de Bolzano, existeix algun punt entre

$c\in (x,b)$

que compleix que

$f(c)=f(a)$

, però això no pot ser perquè

$f$

és injectiva. Pel mateix argument no es pot donar el cas que

$f(a)>f(b)>f(x)$

, ja que existiria algun punt

$c$

que compleix que

$f(c)=f(b)$

. Per tant, tenim que

$f(x)$

està entre

$f(a)$

i

$f(b)$

.

Considerem ara un punt $y\in (x,b)$, és a dir, $a<x<y<b$, pel mateix argument que a dalt podem afirmar que $f(x)>f(y)>f(b)$ (i, per tant, $f(a)>f(x)>f(y)>f(b)$). Per tant, podem afirmar que si $x<y⟹f(x)>f(y)$, és a dir, $f$ és estrictament decreixent, si en comptes de suposar al principi que $f(a)>f(b)$ suposem que $f(a)<f(b)$ arribem a la conclusió (després de aplicar exactament el mateix raonament) que $f$ és estrictament creixent. Demostrem ara que $f^{-1}$ és contínua a l'interval $f(I)$.

Sigui $y_i=f(x_i)\in f(I)$, hem de demostrar que $\mathrm{\forall }ϵ>0,\mathrm{\exists }\delta >0|d(f(x),f(x_i))<\delta ⟹d(f^{-1}(f(x)),f^{-1}(f(x_i)))=d(x,x_i)<ϵ$.

Notem que, en ser $f$ contínua i estrictament creixent (decreixent) es compleix que $f([a,b])=[f(a),f(b)]$ $(=[f(b),f(a)])$. És a dir, que un punt pertany a l'interval $[a,b]$ si i només si la seva imatge pertany a l'interval d'extrems $f(a)$ i $f(b)$.

Per tant, per a qualsevol $ϵ$ podem trobar un $\delta <ϵ$ tal que $[y_i-\delta ,y_i+\delta ]=[f(x_i)-\delta ,f(x_i)+\delta ]\subset [f(x_i)-ϵ,f(x_i)+ϵ]=f([x_i-ϵ,x_i+ϵ]).$

Si $d(f(x),f(x_i))<\delta$, aleshores $f(x)\in [f(x_i)-\delta ,f(x_i)+\delta ]⟹f(x)\in f([x_i-ϵ,x_i+ϵ])⟹x\in [x_i-ϵ,x_i+ϵ]⟹d(x,x_i)<ϵ$

Quedant demostrat que la funció $f^{-1}$ és contínua.

Tipus de discontinuïtats de funcions d'una variable real

Discontinuïtat asimptòtica

En contextos informals, com ara els estudis de batxillerat, es diu que una funció $f(x)$ de domini $D⊊ℝ$ presenta una discontinuïtat asimptòtica en un punt d'acumulació $a\in ̸D$ quan un o tots dos límits laterals de la funció en aquest punt són de tipus infinit. Es pot donar un dels quatre casos diferents:

(1) $\underset{x\to a}{\lim }f(x)=\mathrm{\infty }$ (2) $\underset{x\to a}{\lim }f(x)=-\mathrm{\infty }$ (3) $\underset{x\to a^{-}}{\lim }f(x)=+\mathrm{\infty }$ i $\underset{x\to a^{+}}{\lim }f(x)=-\mathrm{\infty }$ (4) $\underset{x\to a^{-}}{\lim }f(x)=-\mathrm{\infty }$ i $\underset{x\to a^{+}}{\lim }f(x)=+\mathrm{\infty }$

La recta x=a s'anomena asímptota vertical.

És molt important esmentar que, formalment i matemàtica, no té sentit parlar d'una discontinuïtat en un punt que no pertany al domini de la funció. El concepte de discontinuïtat asimptòtica neix del tractament poc rigorós que es fa del concepte de continuïtat a partir de límits, per no haver d'abordar la definició formal vista anteriorment.

Exemple:

Discontinuïtat asimptòtica

Discontinuïtat de salt

Una funció $f(x)$ de domini $D\subseteq ℝ$ presenta una discontinuïtat de salt en un punt $a\in D$ quan els límits laterals en aquest punt no són iguals:

$\underset{x\to a^{-}}{\lim }f(x)\ne \underset{x\to a^{+}}{\lim }f(x)$

Exemple:

Discontinuïtat de salt

Discontinuïtat evitable

Una funció $f(x)$ de domini $D\subseteq ℝ$ presenta una discontinuïtat evitable en un punt $a\in D$ quan la funció té límit en aquest punt però no coincideix amb el valor de la funció: $\underset{x\to a^{-}}{\lim }f(x)=\underset{x\to a^{+}}{\lim }f(x)=\underset{x\to a}{\lim }f(x)\ne f(a)$

Per tant, la funció f es podria fer contínua només redefinint $f(a)$.

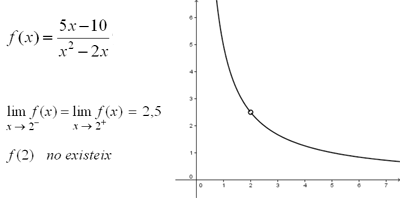
En contextos informals, com ara els estudis de batxillerat, es parla també de discontinuïtats evitables en punts $a\in ̸D$ quan $\underset{x\to a^{-}}{\lim }f(x)=\underset{x\to a^{+}}{\lim }f(x)$. Altra vegada és molt important esmentar que, formalment i matemàtica, no té sentit parlar d'una discontinuïtat en un punt que no pertany al domini de la funció.

Exemple en un context informal (punt fora del domini):

Discontinuïtat evitable

Àlgebra de les funcions contínues i composició de funcions contínues

Per definició:

$f$ contínua a $a\iff \underset{x\to a}{\lim }f(x)=f(a)$.

Dels teoremes sobre els límits resulta:

Àlgebra de les funcions contínues

Siguin $f$ i $g$ dues funcions contínues en un mateix interval $I$. Llavors:

• $\alpha f+\beta g\mathrm{\forall }(\alpha ,\beta )\in {ℝ}^2$ (combinació lineal)
• $f\cdot g$ (producte)
• $\frac{f}{g}(g\ne 0)$ (quocient)

són funcions contínues a $I$.

Composició de funcions contínues

Si $f$ és contínua a $I$ i $g$ és contínua a $f(I)$ llavors $g\circ f$ és contínua a $I$.

Funcions contínues entre espais topològics

La definició esmentada de funció contínua es pot expressar de forma més general a les funcions entre dos espais topològics; donada una funció $f:A⟶B$ entre dos espais topològics, aquesta és contínua si i només si per a tot obert $O\subseteq B$ es dona que $f^{-1}\left[O\right]$ és un obert de $A$.

Vegeu també

• Mètodes infinitesimals