Identitat de Beltrami

Eugenio Beltrami (1835-1900)

La identitat de Beltrami, que porta el nom del matemàtic italià Eugenio Beltrami, és un cas especial de les equacions d'Euler-Lagrange en el càlcul de variacions.

Les equacions d'Euler-Lagrange serveixen per extremar l'acció de les funcions de la forma

$I[u]=\underset{a}{\overset{b}{\int }}L[x,u(x),u^{\prime }(x)]dx,$

on $a$ i $b$ són constants, i $u^{\prime }(x)=\frac{du}{dx}$.

Si $\frac{\partial L}{\partial x}=0$, llavors les equacions d'Euler-Lagrange es redueixen a la identitat de Beltrami,

Plantilla:Equation box 1 on Plantilla:Math és una constant.

Derivació

La següent derivació de la identitat de Beltrami comença amb l'equació d'Euler-Lagrange,

$\frac{\partial L}{\partial u}=\frac{d}{dx}\frac{\partial L}{\partial u^{\prime }}.$

Multiplicant els dos costats per Plantilla:Math,

$u^{\prime }\frac{\partial L}{\partial u}=u^{\prime }\frac{d}{dx}\frac{\partial L}{\partial u^{\prime }}.$

Segons la regla de la cadena,

$\frac{dL}{dx}=\frac{\partial L}{\partial u}{u}^{\prime }+\frac{\partial L}{\partial u^{\prime }}{u}^{″}+\frac{\partial L}{\partial x},$

on $u^{″}=\frac{d{u}^{\prime }}{dx}=\frac{d^{2}u}{d{x}^2}$.

Reordenant això es produeixen

$u^{\prime }\frac{\partial L}{\partial u}=\frac{dL}{dx}-\frac{\partial L}{\partial u^{\prime }}{u}^{″}-\frac{\partial L}{\partial x}.$

Per tant, substituint aquesta expressió per $u^{\prime }\frac{\partial L}{\partial u}$ en la segona equació d'aquesta derivació,

$\frac{dL}{dx}-\frac{\partial L}{\partial u^{\prime }}{u}^{″}-\frac{\partial L}{\partial x}-u^{\prime }\frac{d}{dx}\frac{\partial L}{\partial u^{\prime }}=0.$

Segons la regla del producte, l'últim terme es reexpressa com a

$u^{\prime }\frac{d}{dx}\frac{\partial L}{\partial u^{\prime }}=\frac{d}{dx}\left(\frac{\partial L}{\partial u^{\prime }}{u}^{\prime }\right)-\frac{\partial L}{\partial u^{\prime }}{u}^{″},$

i reordenant,

$\frac{d}{dx}\left(L-u^{\prime }\frac{\partial L}{\partial u^{\prime }}\right)=\frac{\partial L}{\partial x}.$

Per al cas de $\frac{\partial L}{\partial x}=0$, això es redueix a

$\frac{d}{dx}\left(L-u^{\prime }\frac{\partial L}{\partial u^{\prime }}\right)=0,$

de manera prenen els resultats de l'antiderivada en la identitat de Beltrami,

$L-u^{\prime }\frac{\partial L}{\partial u^{\prime }}=C,$

on Plantilla:Math és una constant.

Aplicacions

Solució al problema de la braquistòcrona

La solució al problema de la braquistòcrona és la cicloide

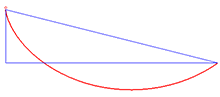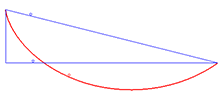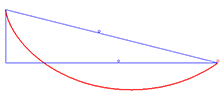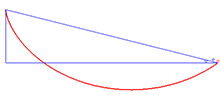
Un exemple d'aplicació de la identitat de Beltrami és el problema de la braquistòcrona, que consisteix a trobar la corba $y=y(x)$ que minimitza la integral

$I[y]=\underset{0}{\overset{a}{\int }}\sqrt{\frac{1+y{\text{'}}^2}{y}}dx.$

L'integrand

$L(y,y^{\prime })=\sqrt{\frac{1+y{\text{'}}^2}{y}}$

no depèn explícitament de la variable d'integració $x$, de manera que s'aplica la identitat de Beltrami,

$L-y^{\prime }\frac{\partial L}{\partial y^{\prime }}=C.$

Substituint per $L$ i simplificant,

$y(1+y{\text{'}}^2)=1/C^2\text{(constant)},$

que es pot resoldre amb el resultat posat en forma d'equacions paramètriques

$x=A(\varphi -\sin \varphi )$

$y=A(1-\cos \varphi )$

amb $A$ sent la meitat de la constant anterior, $\frac{1}{2C^2}$, i $\varphi$ essent una variable. Aquestes són les equacions paramètriques per a una cicloide.