Notació de Voigt

Notació de Voigt per una matriu simètrica 3x3.

S'anomena notació de Voigt al conveni que permet reduir el nombre d'índexs usats per descriure un tensor simètric. Aquesta notació permet, en particular, representar en forma matricial tensors d'ordre 3, com el tensor piezoelècric, o d'ordre 4 com el tensor del mòduls elàstics. Aquesta notació deu el seu nom a Woldemar Voigt que la va elaborar.

Principi i exemple

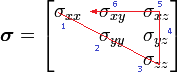
El principi de la notació de Voigt s'il·lustra en el cas de tensors simètrics de rang 2, com el tensor de tensions o el tensor deformació. Es representa el tensor amb una matriu simètrica 3x3:

$\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)$

Aquesta matriu conté 9 coeficients, dels quals només 6 són independents. La matriu donada amb els 6 coeficients representa, doncs, el tensor completament. Es reordena els índexs repetits en un de sol segons el conveni:

$\begin{array}{c}11⟶132\mathrm{o}23⟶4\\ 22⟶231\mathrm{o}13⟶5\\ 33⟶321\mathrm{o}12⟶6\\ \end{array}$

Tanmateix, no es pot simplement substituir els índexs pels índexs contrets. Per tal de guardar una representació coherent amb les propietats físiques, cal introduir alguns factors multiplicatius. Això es pot evidenciar amb un exemple. Es considera la llei de Hooke que relaciona el tensor deformació ${\epsilon }_{ij}$ amb el tensor de tensions ${\sigma }_{kl}$ a través d'un tensor de mòduls elàstics $C_{ijkl}$ :

${\sigma }_{ij}=C_{ijkl}{\epsilon }_{kl}$

S'eescriurà doncs, per exemple per ${\sigma }_{13}$ :

$\begin{array}{cc}{\sigma }_{13}=& C_{1311}{\epsilon }_{11}+C_{1322}{\epsilon }_{22}+C_{1333}{\epsilon }_{33}\\ & +\underset{2C_{1332}{\epsilon }_{32}}{\underbrace{C_{1332}{\epsilon }_{32}+C_{1323}{\epsilon }_{23}}}+\underset{2C_{1331}{\epsilon }_{31}}{\underbrace{C_{1331}{\epsilon }_{31}+C_{1313}{\epsilon }_{13}}}+\underset{2C_{1321}{\epsilon }_{21}}{\underbrace{C_{1312}{\epsilon }_{12}+C_{1321}{\epsilon }_{21}}}\\ \end{array}$

És, doncs, necessari tenir en compte aquests coeficients 2 a l'hora d'escriure aquesta relació mitjançant els índexs contrets:

${\sigma }_5=C_{51}{\epsilon }_1+C_{52}{\epsilon }_2+C_{53}{\epsilon }_3+C_{54}{\epsilon }_4+C_{55}{\epsilon }_5+C_{56}{\epsilon }_6$

En aquest cas, aquest coeficient 2 s'integra per conveni en la definició del tensor deformació, de tal manera que es passa de la notació completa a la notació de Voigt a través de les relacions següents, on es noten els índexs cotrets per lletres gregues.

$\begin{array}{cc}{\sigma }_{\alpha }& ={\sigma }_{ij}\\ C_{\alpha \beta }& =C_{ijkl}\\ {\epsilon }_{\alpha }& ={\epsilon }_{ij}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{r}\alpha =1,2,3\\ & =2{\epsilon }_{ij}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{r}\alpha =4,5,6\\ \end{array}$

Casos usuals

La taula següent mostra els casos usuals d'ús de la notació de Voigt:

Tensor deformació	${\epsilon }_{\alpha }=2^p{\epsilon }_{ij}$
Tensor de tensions	${\sigma }_{\alpha }={\sigma }_{ij}$
Tensors piezoelèctrics	$d_{i\alpha }=2^p{d}_{i(jk)};e_{i\alpha }=e_{i(jk)}$ $g_{i\alpha }=2^p{g}_{i(jk)};h_{i\alpha }=h_{i(jk)}$
Tensor de constants elàstiques	$C_{\alpha \beta }=C_{(ij)(kl)}$
Tensor de compliàncices elàstiques	$S_{\alpha \beta }=2^p{S}_{(ij)(kl)}$
Per cada cop, $p$ és el nombre d'índexs contrets iguals a 4, 5 o 6