Topologia quocient

La cinta de Möbius es pot veure com un espai topològic quocient (veure el segon exemple).

En matemàtiques, la topologia quocient és una topologia definida sobre el conjunt quocient generat per una relació d'equivalència sobre un espai topològic.

Definició

Siga $(X,{𝒯}_X)$ un espai topològic i $ℛ$ una relació d'equivalència sobre $X$. El conjunt quocient $X/ℛ$ és el conjunt de les classes d'equivalència dels elements de $X$:

$X/ℛ=\{[x]:x\in X\}$

Els conjunts oberts que conforman l'anomenada topologia quocient sobre $X/ℛ$ són els conjunts de las classes d'equivalència les unions de les quals són conjunts oberts en $X$:

${𝒯}_{ℛ}=\{U\subseteq X/ℛ:\bigcup _{[x]\in U}[x]\subseteq {𝒯}_X\}.$

Definició equivalent: sigui $p:X\to X/ℛ$ l'aplicació projecció donada per $p(x)=[x]$, aleshores es defineixen els oberts de ${𝒯}_{ℛ}$ com els conjunts $U\subseteq Y$ tals que $p^{-1}(U)\subseteq X$ és obert en $X$.

Propietats

• L'aplicació $p:X\to X/ℛ$ que envia a cada element a la seva classe d'equivalència corresponent és continua.
• Siguen $p:X\to X/ℛ$ la projecció i $\phi :X/ℛ\to Y$. L'aplicació $\phi$ és continua si, i només si, la composició $\phi \circ p:X\to Y$ és continua.

Exemples

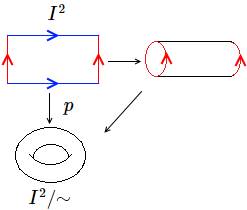
• El tor com a conjunt quocient: Sobre $I^2=[0,1]\times [0,1]$ es defineix la relació d'equivalència $(x,0)ℛ(x,1)$ i $(0,y)ℛ(1,y)$. L'espai quocient $I^2/ℛ$ és homeomorf a un tor.

Tor

• La cinta de Möbius com a conjunt quocient: Sobre $I^2$ es defineix la relació d'equivalència $(0,y)ℛ(1,1-y)$. L'espai quocient $I^2/ℛ$ és homeomorf a una cinta de Möbius.

Banda de Möbius

• La ampolla de Klein com a conjunt quocient: Sobre $I^2$ es defineix la relació d'equivalència $(x,0)ℛ(x,1)$ i $(0,y)ℛ(1,1-y)$. L'espai quocient $I^2/ℛ$ és homeomorf a una ampolla de Klein (es difícil de visualitzar ja que no és homeomorf a un subespai de ${ℝ}^3$).

• L'esfera com a conjunt quocient: Sobre $\{(x,y):|x|+|y|\le 1\}$ es defineix la relació d'equivalència $(x,y)ℛ(-x,y)$ per a $(x,y)$ de la frontera. L'espai quocient corresponent és homeomorf a una esfera.

Vegeu també

• Conjunt quocient
• Homeomorfisme
• Espai topològic

Bibliografia

• Robles Corbalá Carlos Alberto, "Topología general", Universitat de Sonora.
• Plantilla:MathWorld
• Plantilla:PlanetMath