Procés de naixement-mort

El procés de naixement i mort (o procés de naixement i mort) és un cas especial de procés de Màrkov de temps continu on les transicions d'estat només són de dos tipus: "naixements", que augmenten la variable d'estat en un i "morts". que disminueixen l'estat en un. Va ser presentat per William Feller. El nom del model prové d'una aplicació comuna, l'ús d'aquests models per representar la mida actual d'una població on les transicions són naixements i morts literals. Els processos de naixement i mort tenen moltes aplicacions en demografia, teoria de les cues, enginyeria del rendiment, epidemiologia, biologia i altres àrees. Es poden utilitzar, per exemple, per estudiar l'evolució dels bacteris, el nombre de persones amb una malaltia dins d'una població o el nombre de clients a la fila al supermercat.

Definició

Quan es produeix un naixement, el procés passa de l'estat n a n + 1. Quan es produeix una mort, el procés va d'estat n a estat n − 1. El procés s'especifica per taxes de natalitat positives $\{{\lambda }_i{\}}_{i=0\dots \mathrm{\infty }}$ i taxes de mortalitat positives $\{{\mu }_i{\}}_{i=1\dots \mathrm{\infty }}$. El nombre d'individus en el procés al mateix temps $t$ es denota per $X(t)$. El procés té la propietat de Màrkov i $P_{i,j}(t)=𝖯\{X(t+s)=j|X(s)=i\}$ descriu com $X(t)$ canvis a través del temps. Per a petits $\mathrm{△}t>0$, la funció $P_{i,j}(\mathrm{△}t)$ se suposa que compleix les propietats següents:

$P_{i,i+1}(\mathrm{△}t)={\lambda }_i\mathrm{△}t+o(\mathrm{△}t),i\ge 0,$

$P_{i,i-1}(\mathrm{△}t)={\mu }_i\mathrm{△}t+o(\mathrm{△}t),i\ge 1,$

$P_{i,i}(\mathrm{△}t)=1-({\lambda }_i+{\mu }_i)\mathrm{△}t+o(\mathrm{△}t),i\ge 1.$

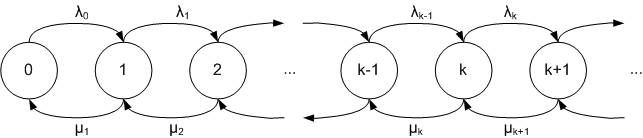
Aquest procés està representat per la figura següent amb els estats del procés (és a dir, el nombre d'individus de la població) representats pels cercles, i les transicions entre estats indicades per les fletxes.

Recurrència i transitorietat

Per a la recurrència i la transitorietat en els processos de Markov, vegeu la Secció 5.3 de la cadena de Màrkov.

Condicions de recurrència i transitorietat

Les condicions per a la recurrència i la transitorietat van ser establertes per Samuel Karlin i James McGregor.

Un procés de naixement i mort és recurrent si i només si

$\sum _{i=1}^{\mathrm{\infty }}\prod _{n=1}^i\frac{{\mu }_n}{{\lambda }_n}=\mathrm{\infty }.$

Un procés de naixement i mort és ergòdic si i només si

$\sum _{i=1}^{\mathrm{\infty }}\prod _{n=1}^i\frac{{\mu }_n}{{\lambda }_n}=\mathrm{\infty }\text{and}\sum _{i=1}^{\mathrm{\infty }}\prod _{n=1}^i\frac{{\lambda }_{n-1}}{{\mu }_n}<\mathrm{\infty }.$

Un procés de naixement i mort és nul-recurrent si i només si

$\sum _{i=1}^{\mathrm{\infty }}\prod _{n=1}^i\frac{{\mu }_n}{{\lambda }_n}=\mathrm{\infty }\text{and}\sum _{i=1}^{\mathrm{\infty }}\prod _{n=1}^i\frac{{\lambda }_{n-1}}{{\mu }_n}=\mathrm{\infty }.$

Mitjançant l'ús de la prova de Bertrand ampliada (vegeu la secció 4.1.4 de Ratio test) les condicions de recurrència, transitorietat, ergodicitat i recurrència nul·la es poden derivar d'una forma més explícita.

Per a nombre sencer $K\ge 1,$ deixar ${\ln }_{(K)}(x)$ denoten el $K$ la iteració del logaritme natural, és a dir ${\ln }_{(1)}(x)=\ln (x)$ i per a qualsevol $2\le k\le K$, ${\ln }_{(k)}(x)={\ln }_{(k-1)}(\ln (x))$.

Aleshores, les condicions per a la recurrència i la transitorietat d'un procés de naixement i mort són les següents.

El procés de naixement i mort és transitori si n'hi ha $c>1,$$K\ge 1$ i $n_0$ tal que per a tots $n>n_0$

$\frac{{\lambda }_n}{{\mu }_n}\ge 1+\frac{1}{n}+\frac{1}{n}\sum _{k=1}^{K-1}\frac{1}{\prod _{j=1}^k{\ln }_{(j)}(n)}+\frac{c}{n\prod _{j=1}^K{\ln }_{(j)}(n)},$

on la suma buida per $K=1$ s'assumeix que és 0.

El procés de naixement i mort és recurrent si n'hi ha $K\ge 1$ i $n_0$ tal que per a tots $n>n_0$

$\frac{{\lambda }_n}{{\mu }_n}\le 1+\frac{1}{n}+\frac{1}{n}\sum _{k=1}^K\frac{1}{\prod _{j=1}^k{\ln }_{(j)}(n)}.$

Es poden trobar classes més àmplies de processos de naixement i mort, per als quals es poden establir les condicions de recurrència i transitorietat.

Aplicació

Considereu la caminada aleatòria unidimensional $S_t,t=0,1,\dots ,$ que es defineix de la següent manera. Deixa $S_0=1$, i $S_t=S_{t-1}+e_t,t\ge 1,$ on $e_t$ pren valors $\pm 1$, i la distribució de $S_t$ es defineix per les condicions següents:

$𝖯\{S_{t+1}=S_t+1|S_t>0\}=\frac{1}{2}+\frac{{\alpha }_{S_t}}{S_t},𝖯\{S_{t+1}=S_t-1|S_t>0\}=\frac{1}{2}-\frac{{\alpha }_{S_t}}{S_t},𝖯\{S_{t+1}=1|S_t=0\}=1,$

on ${\alpha }_n$ satisfer la condició $0<{\alpha }_n<\min \{C,n/2\},C>0$.

El passeig aleatori descrit aquí és un anàleg de temps discret del procés de naixement i mort (vegeu la cadena de Màrkov) amb les taxes de natalitat

$lambd{a}_n=\frac{1}{2}+\frac{{\alpha }_n}{n},$

i les taxes de mortalitat

${\mu }_n=\frac{1}{2}-\frac{{\alpha }_n}{n}$