Prova de khi quadrat

Distribució χ², amb Plantilla:Math a l'eix x i el valor p (probabilitat de la cua dreta) a l'eix y.

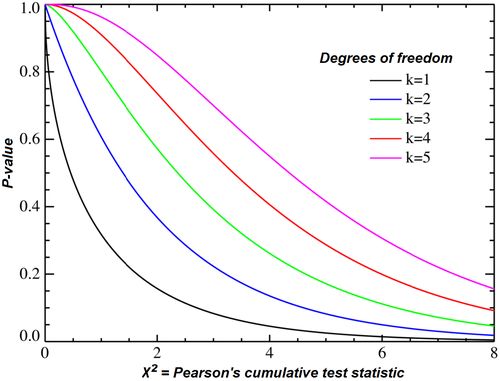
En estadística i estadística aplicada es denomina prova de khi quadrat (pronunciat [xi]Plantilla:Efn) o prova de χ² a qualsevol contrast d'hipòtesis en el qual l'estadístic utilitzat segueix una distribució χ² si la hipòtesi nul·la és certa. Alguns exemples de proves χ² són els següents:

• La prova de khi-quadrat de Pearson, la qual té nombroses aplicacions:

• La prova χ² de freqüències.
• La prova χ² d'independència.
• La prova χ² de bondat d'ajust.

• La prova de khi-quadrat de Pearson amb correcció per continuïtat o correcció de Yates.
• La prova de Bartlett d'homogeneïtat de variàncies.

La prova és vàlida quan l'estadística de la prova és distribuïda khi quadrat sota la hipòtesi nul·la, específicament prova de khi quadrat de Pearson i variants d'aquesta. La prova de khi-quadrat de Pearson s'utilitza per a determinar si existeix una diferència estadísticament significativa entre la freqüència esperada i les freqüències observades en una o més categories d'una taula de contingència. Per a taules de contingència amb grandàries de mostra més petites s'utilitza en el seu lloc una prova exacta de Fisher.

En les aplicacions estàndard d'aquesta prova, les observacions es classifiquen en classes mútuament excloents. Si la hipòtesi nul·la segons la qual no hi ha diferències entre les classes de la població és certa, l'estadística de prova calculada a partir de les observacions segueix una distribució de freqüències Plantilla:Math. El propòsit de la prova és avaluar quina probabilitat tindrien les freqüències observades suposant que la hipòtesi nul·la fos certa.

Els estadístics de prova que segueixen una distribució Plantilla:Math ocorren quan les observacions són independents. També hi ha proves Plantilla:Math per a provar la hipòtesi nul·la d'independència d'un parell de variables aleatòries basades en observacions dels parells.

El terme prova de khi quadrat sol referir-se a proves en les quals la distribució de l'estadístic de prova s'aproxima a la distribució Plantilla:Math de forma asimptòtica, la qual cosa significa que la distribució mostral (si la hipòtesi nul·la és una certa) de l'estadístic de prova s'aproxima cada vegada més a una distribució khi quadrat a mesura que augmenten les grandàries de mostra.

Història

Al Plantilla:Segle, els mètodes d'anàlisi estadística s'aplicaven principalment en l'anàlisi de dades biològiques i era habitual que els investigadors assumissin que les observacions seguien una distribució normal, tal com feren Sir George Airy i Mansfield Merriman, els treballs dels quals van ser criticats per Karl Pearson al un article seu de 1900.

A la finals del segle XIX, Pearson es va adonar de l'existència d'una asimetria significativa en algunes observacions biològiques. Per a modelar les observacions independentment que fossin normals o esbiaixades, Pearson, en una sèrie d'articles publicats entre 1893 i 1916, va desenvolupar la distribució de Pearson, una família de distribucions de probabilitat contínua que inclou la distribució normal i nombroses distribucions esbiaixades, i va proposar un mètode d'anàlisi estadística consistent a utilitzar la distribució de Pearson per a modelar les observacions i realitzar proves de bondat d'ajust per a determinar si un model s'ajusta a les observacions.

Prova de khi quadrat de Pearson

Plantilla:AP El 1900 Pearson va publicar un treball sobre la prova Plantilla:Math que és considerat una de les pedres fundacionals de l'estadística moderna. En aquest treball, Pearson va investigar una prova de bondat d'ajust.

Suposi's que Plantilla:Mvar observacions d'una mostra aleatòria d'una població es classifiquen en Plantilla:Mvar classes mútuament exclusives amb nombres observats respectius Plantilla:Mvar (per a Plantilla:Math), i una hipòtesi nul·la dona la probabilitat Plantilla:Mvar que una observació caigui dintre la classe Plantilla:Mvar-èsima. S'obté, per tant, els nombres esperants Plantilla:Math per a tot Plantilla:Mvar, on:

$\begin{array}{cc}& \sum _{i=1}^k{p}_i=1\\ & \sum _{i=1}^k{m}_i=n\sum _{i=1}^k{p}_i=n\end{array}$

Pearson proposà que, sota la circumstància que la hipòtesi nul·la sigui correcta, si Plantilla:Math la distribució limitant de la quantitat de sota és la distribució Plantilla:Math.

$X^2=\sum _{i=1}^k\frac{(x_i-m_i{)}^2}{m_i}=\sum _{i=1}^k\frac{x_i^2}{m_i}-n$

Pearson tractà primer el cas en el qual els nombres esperants Plantilla:Mvar són nombres prou grans i coneguts en totes les cel·les assumint que tota observació Plantilla:Mvar es pugui considerar normalment distribuïda, i arribà al resultat que, al límit quan Plantilla:Mvar esdevé molt gran, X² segueix la distribució Plantilla:Math amb Plantilla:Math graus de llibertat.

Tanmateix, a continuació Pearson considerà el cas en el qual els nombres esperats depenen dels paràmetres a estimar a partir de la mostra, i suggerí que, amb la notació de Plantilla:Mvar sent els nombres esperats verdaders i Plantilla:Math sent els nombres esperats estimats, la diferència

$X^2-{X^{\prime }}^2=\sum _{i=1}^k\frac{x_i^2}{m_i}-\sum _{i=1}^k\frac{x_i^2}{m{\text{'}}_i}$

usualment seria positiva i prou petita per a poder omesa. En conclusió, Pearson argumentà que si es mira X² també distribuïda com una distribució Plantilla:Math amb Plantilla:Math graus de llibertat, l'error d'aquesta aproximació no afecta les decisions pràctiques. Aquesta conclusió causà una mica de controvèrsia en aplicacions pràctiques i no es resolgué definitivament fins al cap de vint anys, amb la publicació dels articles de Fisher de 1922 i 1924.

Altres exemples de proves de khi quadrat

Un estadístic de prova que segueix una distribució khi quadrat de manera exacta és el test que la variància d'una població normalment distribuïda té un cert valor basat en una variància mostral. Aquests tests són poc comuns a la pràctica perquè normalment es desconeix la variància real de la població. Tanmateix existeixen moltes proves estadítsiques en les quals la distribució khi quadrat és aproximadament vàlida:

Prova exacta de Fisher

Per a la prova exacta utilitzada en lloc de la prova de khi quadrat 2 × 2 d'independència, vegeu Prova exacta de Fisher.

Prova binomial

Per a la prova exacta utilitzada en lloc de la prova de khi quadrat 2 × 1 de bondat d'ajust, vegeu Prova binomial.

Altres proves de khi quadrat

• Prova de khi quadrat de Cochran–Mantel–Haenszel.
• Prova de McNemar, utilitzada en algunes taules Plantilla:Nowrap amb aparellament.
• Prova d'addictivitat de Tukey.
• Prova portmanteau en anàlisi de sèries temporals per a detectar la presència d'autocorrelació.
• Prova de raó de versemblança en modelitzat estadístic general, per provar si hi ha evidència de la necessitat de moure d'un model simple a un de més complicat.

Exemple de prova de khi quadrat per a dades categòriques

Suposi's que hi ha una ciutat amb 1.000.000 de residents amb quatre veïnats Plantilla:Math, Plantilla:Math, Plantilla:Math i Plantilla:Math. Es pren una mostra aleatòria de 650 residents de la ciutat i es classifiquen segons el tram de renda econòmica «baixa», «mitjana» o «alta». La hipòtesi nul·la és que el veïnat de residència de cada persona és independent de la seva posició de tram de renda econòmica. Les dades es troben tabulades en la següent taula:

	Plantilla:Math	Plantilla:Math	Plantilla:Math	Plantilla:Math	Total
Renda baixa	90	60	104	95	349
Renda mitjana	30	50	51	20	151
Renda alta	30	40	45	35	150
Total	150	150	200	150	650

Prengui's la mostra de les persones que viuen al veïnat Plantilla:Math, 150, per tal d'estimar quina proporció del total d'1.000.000 habitants viuen al veïnat Plantilla:Math. De la mateixa manera, calculi's Plantilla:Sfrac per a estimar quina proporció dels 1.000.000 habitants són de renda baixa. Per assumpció d'independència sota la hipòtesi nul·la s'hauria d'"esperar" que el nombre de persones de «renda baixa» al veïnat Plantilla:Math són:

$150\times \frac{349}{650}\approx 80.54$

En aquesta cel·la de la taula es té que:

$\frac{{(\text{observat}-\text{esperat})}^2}{\text{esperat}}=\frac{{(90-80.54)}^2}{80.54}\approx 1.11$

La suma d'aquestes quantitats sobre totes les cel·les és l'estadístic de prova; en aquest cas, $\approx 24.57$. Sota la hipòtesi nul·la, aquesta suma té aproximadament una distribució de khi quadrat amb el següent nombre de graus de llibertat:

$(\text{nombre de files}-1)(\text{nombre de columnes}-1)=(3-1)(4-1)=6$

Si l'estadístic de prova és improbablement gran segons aquesta distribució de khi quadrat, es rebutja la hipòtesi nul·la d'independència.

Bibliografia

• Plantilla:MathWorld
• Plantilla:Citar ref
• Plantilla:Citar ref
• Plantilla:Citar ref
• Plantilla:Citar ref

Enllaços externs

• Chi-Square Calculator from GraphPad
• Chi-Square Test in QtiPlot
• Vassar College 's 2 × 2 Chi-Square with Expected Values