Funció zeta de Hurwitz

En matemàtiques, la funció zeta de Hurwitz, anomenada així per Adolf Hurwitz, és una de les moltes funcions zeta. Es defineix formalment per a arguments complexos s amb Re(s) > 1 i q amb Re(q) > 0 per a

$\zeta (s,q)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{(q+n{)}^s}.$

Aquesta sèrie és absolutament convergent per als valors donats de s i q i es pot estendre a una funció meromorfa definida per a tot s≠1. La funció zeta de Riemann és ζ(s,1).

Continuació analítica

Si $\mathrm{R}\mathrm{e}(s)\le 1$ la funció zeta de Hurwitz es pot definir per l'equació

$\zeta (s,q)=\mathrm{\Gamma }(1-s)\frac{1}{2\pi i}\underset{C}{\int }\frac{z^{s-1}{e}^{qz}}{1-e^z}dz$

on el contorn $C$ és un llaç al voltant de l'eix real negatiu. Això proporciona una continuació analítica de $\zeta (s,q)$.

• 
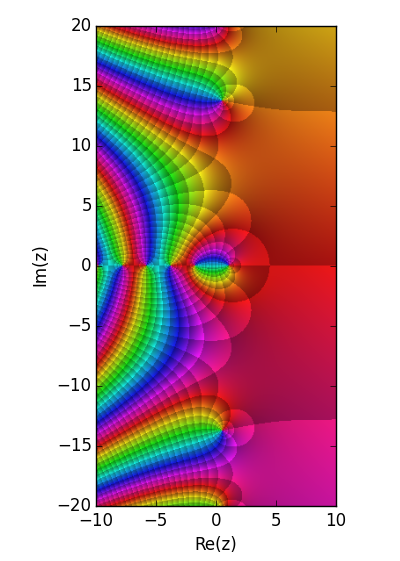
  Funció zeta de Hurwitz corresponent a Plantilla:Nowrap. Es genera com a graf Matplotlib mitjançant una versió del mètode de coloració de dominis.
• 
  Funció zeta de Hurwitz corresponent a Plantilla:Nowrap

La funció zeta de Hurwitz es pot ampliar mitjançant la continuació analítica a una funció meromorfa definida per a tots els complexos $s$ amb $s\ne 1$. A $s=1$ té un pol simple amb residu $1$. El terme constant ve donat per

$\underset{s\to 1}{\lim }[\zeta (s,q)-\frac{1}{s-1}]=\frac{-{\mathrm{\Gamma }}^{\prime }(q)}{\mathrm{\Gamma }(q)}=-\psi (q)$

on $\mathrm{\Gamma }$ és la funció gamma i $\psi$ és la funció digamma.

Representació en sèries

Funció zeta de Hurwitz com a funció q amb Plantilla:Nowrap.

Una representació convergent de la sèrie de Newton definida per a q > 0 (real) i qualsevol complex s ≠ 1 va ser donada per Helmut Hasse el 1930:

$\zeta (s,q)=\frac{1}{s-1}\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n+1}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(q+k{)}^{1-s}.$

Aquesta sèrie convergeix uniformement en subconjunts compactes del pla s a tota una funció. Es pot entendre que la suma interior és l'enèsima diferència posterior de $q^{1-s}$; això és,

${\mathrm{\Delta }}^n{q}^{1-s}=\sum _{k=0}^n(-1{)}^{n-k}(\genfrac{}{}{0ex}{}{n}{k})(q+k{)}^{1-s}$

on Δ és l'operador de diferència posterior. Així, es pot escriure

$\begin{array}{cc}\zeta (s,q)& =\frac{1}{s-1}\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{n+1}{\mathrm{\Delta }}^n{q}^{1-s}\\ & =\frac{1}{s-1}\frac{\log (1+\mathrm{\Delta })}{\mathrm{\Delta }}{q}^{1-s}\end{array}$

Altres exemples que convergeixen a nivell global inclouen aquests exemples

$\zeta (s,v-1)=\frac{1}{s-1}\sum _{n=0}^{\mathrm{\infty }}{H}_{n+1}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(k+v{)}^{1-s}$

$\zeta (s,v)=\frac{k!}{(s-k{)}_k}\sum _{n=0}^{\mathrm{\infty }}\frac{1}{(n+k)!}\left[\genfrac{}{}{0ex}{}{n+k}{n}\right]\sum _{l=0}^{n+k-1}(-1{)}^l(\genfrac{}{}{0ex}{}{n+k-1}{l})(l+v{)}^{k-s},k=1,2,3,\dots$

$\zeta (s,v)=\frac{v^{1-s}}{s-1}+\sum _{n=0}^{\mathrm{\infty }}|G_{n+1}|\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(k+v{)}^{-s}$

$\zeta (s,v)=\frac{(v-1{)}^{1-s}}{s-1}-\sum _{n=0}^{\mathrm{\infty }}{C}_{n+1}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(k+v{)}^{-s}$

$\zeta (s,v)(v-\frac{1}{2})=\frac{s-2}{s-1}\zeta (s-1,v)+\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n{G}_{n+2}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(k+v{)}^{-s}$

$\zeta (s,v)=-\sum _{l=1}^{k-1}\frac{(k-l+1{)}_l}{(s-l{)}_l}\zeta (s-l,v)+\sum _{l=1}^k\frac{(k-l+1{)}_l}{(s-l{)}_l}{v}^{l-s}+k\sum _{n=0}^{\mathrm{\infty }}(-1{)}^n{G}_{n+1}^{(k)}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})(k+v{)}^{-s}$

on Plantilla:Math són els nombres Harmònics, $\left[\genfrac{}{}{0ex}{}{\cdot }{\cdot }\right]$ són els nombres de Stirling de primera espècie, $(\dots {)}_{\dots }$ és el símbol de Pochhammer, Plantilla:Math són els coeficients de Gregory, Plantilla:Math són els coeficients de Gregori d'ordre superior i Plantilla:Math són els nombres de Cauchy de segona espècie (Plantilla:Math, Plantilla:Math, Plantilla:Math…).

Representació integral

La funció té una representació integral en termes de la transformada de Mellin com

$\zeta (s,q)=\frac{1}{\mathrm{\Gamma }(s)}\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{t^{s-1}{e}^{-qt}}{1-e^{-t}}dt$

per a $\mathrm{\Re }s>1$ i $\mathrm{\Re }q>0.$

La fórmula de Hurwitz

La fórmula de Hurwitz és el teorema que

$\zeta (1-s,x)=\frac{1}{2s}[e^{-i\pi s/2}\beta (x;s)+e^{i\pi s/2}\beta (1-x;s)]$

on

$\beta (x;s)=2\mathrm{\Gamma }(s+1)\sum _{n=1}^{\mathrm{\infty }}\frac{\exp (2\pi inx)}{(2\pi n{)}^s}=\frac{2\mathrm{\Gamma }(s+1)}{(2\pi {)}^s}{\text{Li}}_s(e^{2\pi ix})$

és una representació de la zeta que és vàlida per a $0\le x\le 1$ i s > 1. Aquí, ${\text{Li}}_s(z)$ és el polilogaritme.

Equació funcional

L'equació funcional relaciona valors de la zeta als costats esquerre i dret del pla complex. Per a nombres enters $1\le m\le n$,

$\zeta (1-s,\frac{m}{n})=\frac{2\mathrm{\Gamma }(s)}{(2\pi n{)}^s}\sum _{k=1}^n[\cos (\frac{\pi s}{2}-\frac{2\pi km}{n})\zeta (s,\frac{k}{n})]$

val per a tots els valors de s.

Algunes sumes finites

Estretament relacionades amb l'equació funcional es troben les sumes finites següents, algunes de les quals es poden avaluar de forma tancada

$\sum _{r=1}^{m-1}\zeta (s,\frac{r}{m})\cos \frac{2\pi rk}{m}=\frac{m\mathrm{\Gamma }(1-s)}{(2\pi m{)}^{1-s}}\sin \frac{\pi s}{2}\cdot \{\zeta (1-s,\frac{k}{m})+\zeta (1-s,1-\frac{k}{m})\}-\zeta (s)$

$\sum _{r=1}^{m-1}\zeta (s,\frac{r}{m})\sin \frac{2\pi rk}{m}=\frac{m\mathrm{\Gamma }(1-s)}{(2\pi m{)}^{1-s}}\cos \frac{\pi s}{2}\cdot \{\zeta (1-s,\frac{k}{m})-\zeta (1-s,1-\frac{k}{m})\}$

$\sum _{r=1}^{m-1}{\zeta }^2(s,\frac{r}{m})=(m^{2s-1}-1){\zeta }^2(s)+\frac{2m{\mathrm{\Gamma }}^2(1-s)}{(2\pi m{)}^{2-2s}}\sum _{l=1}^{m-1}\{\zeta (1-s,\frac{l}{m})-\cos \pi s\cdot \zeta (1-s,1-\frac{l}{m})\}\zeta (1-s,\frac{l}{m})$

on m és enter positiu major de 2 i s és complex (vegeu, per exemple, Apèndix B a Blagouchine, 2014)

Sèries de Taylor

La derivada de la zeta en el segon argument és un canvi:

$\frac{\partial }{\partial q}\zeta (s,q)=-s\zeta (s+1,q).$

Així, la sèrie de Taylor es pot escriure com:

$\zeta (s,x+y)=\sum _{k=0}^{\mathrm{\infty }}\frac{y^k}{k!}\frac{{\partial }^k}{\partial x^k}\zeta (s,x)=\sum _{k=0}^{\mathrm{\infty }}(\genfrac{}{}{0ex}{}{s+k-1}{s-1})(-y{)}^k\zeta (s+k,x).$

Alternativament,

$\zeta (s,q)=\frac{1}{q^s}+\sum _{n=0}^{\mathrm{\infty }}(-q{)}^n(\genfrac{}{}{0ex}{}{s+n-1}{n})\zeta (s+n),$

amb $|q|<1$.

Estretament relacionada està la fórmula Stark–Keiper:

$\zeta (s,N)=\sum _{k=0}^{\mathrm{\infty }}[N+\frac{s-1}{k+1}](\genfrac{}{}{0ex}{}{s+k-1}{s-1})(-1{)}^k\zeta (s+k,N)$

que manté per a N senceres i s arbitràris. Vegeu també la fórmula de Faulhaber per a una relació similar sobre sumes finites de potències d'enters.

Sèries de Laurent

L'expansió de la sèrie de Laurent es pot utilitzar per definir les constants de Stieltjes que es produeixen a la sèrie

$\zeta (s,q)=\frac{1}{s-1}+\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{n!}{\gamma }_n(q)(s-1{)}^n.$

Concretament ${\gamma }_0(q)=-\psi (q)$ i ${\gamma }_0(1)=-\psi (1)={\gamma }_0=\gamma$.

Transformada de Fourier

La transformada discreta de Fourier de la funció zeta de Hurwitz respecte de l'ordre s és la funció khi de Legendre.

Relació amb els polinomis de Bernoulli

La funció $\beta$ definida anteriorment generalitza els polinomis de Bernoulli:

$B_n(x)=-\mathrm{\Re }[(-i{)}^n\beta (x;n)]$

on $\mathrm{\Re }z$ denota la part real de z. Alternativament,

$\zeta (-n,x)=-\frac{B_{n+1}(x)}{n+1}.$

En particular, la relació es manté $n=0$ i s'obté

$\zeta (0,x)=\frac{1}{2}-x.$

Relacions amb altres funcions

Relació amb la funció theta de Jacobi

Si $\vartheta (z,\tau )$ és la funció theta de Jacobí

$\underset{0}{\overset{\mathrm{\infty }}{\int }}[\vartheta (z,it)-1]t^{s/2}\frac{dt}{t}={\pi }^{-(1-s)/2}\mathrm{\Gamma }\left(\frac{1-s}{2}\right)[\zeta (1-s,z)+\zeta (1-s,1-z)]$

es sosté per a $\mathrm{\Re }s>0$ i z complex, però no un nombre enter. Per a un nombre enter z=n, això simplifica

$\underset{0}{\overset{\mathrm{\infty }}{\int }}[\vartheta (n,it)-1]t^{s/2}\frac{dt}{t}=2{\pi }^{-(1-s)/2}\mathrm{\Gamma }\left(\frac{1-s}{2}\right)\zeta (1-s)=2{\pi }^{-s/2}\mathrm{\Gamma }\left(\frac{s}{2}\right)\zeta (s).$

on ζ és la funció zeta de Riemann. Tingueu en compte que aquesta última forma és l'equació funcional de la funció zeta de Riemann, donada originalment per Riemann. La distinció basada en que z sigui un nombre enter o no té en compte que la funció theta de Jacobi convergeix a la funció delta periòdica, o pinta de Dirac, en z com a $t\to 0$.

Relació amb les funcións L de Dirichlet

Per arguments racionals, la funció zeta de Hurwitz es pot expressar com una combinació lineal de funcions L de Dirichlet i viceversa: la funció zeta de Hurwitz coincideix amb la funció zeta de Riemann ζ(s) quan q = 1, quan q = 1/2és igual a (2^s−1)ζ(s), i si q = n/k amb k > 2, (n,k) > 1 i 0 < n < k, llavors

$\zeta (s,n/k)=\frac{k^s}{\phi (k)}\sum _{\chi }\bar{\chi }(n)L(s,\chi ),$

la suma que corre sobre tots els caràcters de Dirichlet mod k. En sentit contrari, tenim la combinació lineal

$L(s,\chi )=\frac{1}{k^s}\sum _{n=1}^k\chi (n)\zeta (s,\frac{n}{k}).$

També hi ha el teorema de multiplicació

$k^s\zeta (s)=\sum _{n=1}^k\zeta (s,\frac{n}{k}),$

de les quals una generalització útil és la relació de distribució

$\sum _{p=0}^{q-1}\zeta (s,a+p/q)=q^s\zeta (s,qa).$

(Aquesta última forma és vàlida sempre que q sigui nombre natural i 1 − qa no ho sigui).

Relació amb la funció poligamma

La funció zeta de Hurwitz generalitza la funció poligamma per ordres $s$ no-senceres :

${\psi }_s(z)=\frac{1}{\mathrm{\Gamma }(-s)}(\frac{\partial }{\partial s}+\psi (-s)+\gamma )\zeta (s+1,z)$

amb la constant d'Euler-Mascheroni $\gamma$.

Derivades

Aplicant

$\frac{{\partial }^n\zeta (s,a)}{\partial s^n}=\frac{(-1{)}^n}{2^n}\sum _{k=0}^{\mathrm{\infty }}\frac{{\log }^n((a+k{)}^2)}{{((a+k{)}^2)}^{s/2}}$

amb $-a\notin \mathbb{N}$ i també $\mathrm{R}\mathrm{e}(s)>1$ i $n\in \mathbb{N}$.

Les derivades respecte $a$ són :

$\frac{{\partial }^n\zeta (s,a)}{\partial a^n}=(1-n-s,n)\sum _{k=0}^{\mathrm{\infty }}\frac{1}{(a+k{)}^n{((a+k{)}^2)}^{s/2}}$

per a $a\notin \mathbb{N}$ i $n\in \mathbb{N}$ utilitzant el Símbol de Pochhammer $(x,n)$.

Zeros

Si q=1, la funció zeta de Hurwitz es redueix a la funció zeta de Riemann.

Si q=1/2, es redueix a la funció zeta de Riemann multiplicada per una funció simple d'argument complex s (vegeu més amunt), donant lloc en cada cas al difícil estudi dels zeros de la funció zeta de Riemann. En particular, no hi haurà zeros amb una part real superior o igual a 1.

Tanmateix, si 0<q<1 i q≠1/20, hi ha zeros de la funció zeta de Hurwitz a la franja 1<Re(s)<1+ε per a qualsevol nombre real positiu ε. Això ho va demostrar Harold Davenport i Hans Heilbronn per a q irracional, racional o transcendent, i per Cassels per q irracional algebraic.

Valors relacionals

Es produeix la funció zeta de Hurwitz en diverses identitats sorprenents a valors racionals. En particular, valors en termes dels polinomis d'Euler $E_n(x)$:

$E_{2n-1}\left(\frac{p}{q}\right)=(-1{)}^n\frac{4(2n-1)!}{(2\pi q{)}^{2n}}\sum _{k=1}^q\zeta (2n,\frac{2k-1}{2q})\cos \frac{(2k-1)\pi p}{q}$

i

$E_{2n}\left(\frac{p}{q}\right)=(-1{)}^n\frac{4(2n)!}{(2\pi q{)}^{2n+1}}\sum _{k=1}^q\zeta (2n+1,\frac{2k-1}{2q})\sin \frac{(2k-1)\pi p}{q}$

També s'obté

$\zeta (s,\frac{2p-1}{2q})=2(2q{)}^{s-1}\sum _{k=1}^q[C_s\left(\frac{k}{q}\right)\cos \left(\frac{(2p-1)\pi k}{q}\right)+S_s\left(\frac{k}{q}\right)\sin \left(\frac{(2p-1)\pi k}{q}\right)]$

que manté $1\le p\le q$. Aquí, el $C_{\nu }(x)$ i $S_{\nu }(x)$ es defineixen mitjançant la funció khi de Legendre ${\chi }_{\nu }$ com

$C_{\nu }(x)=\mathrm{Re}{\chi }_{\nu }(e^{ix})$

i

$S_{\nu }(x)=\mathrm{Im}{\chi }_{\nu }(e^{ix}).$

Per a valors enters de ν, aquests poden ser expressats en termes dels polinomis d'Euler. Aquestes relacions es poden derivar mitjançant l'equació funcional juntament amb la fórmula de Hurwitz, que es dona més amunt.

Aplicacions

La funció zeta de Hurwitz es presenta en diverses disciplines. El més comú es dona en la teoria de nombres, on la seva teoria és la més profunda i desenvolupada. Tot i això, també es produeix en l'estudi de fractals i sistemes dinàmics. En estadístiques aplicades, es produeix en la llei de Zipf i la llei Zipf-Mandelbrot. En física de partícules es produeix en una fórmula de Julian Schwinger, donant un resultat exacte per a la taxa de creació de parells d'un electró Dirac en un camp elèctric uniforme.

Casos especials i generalitzacions

La funció zeta de Hurwitz amb un nombre enter positiu m està relacionada amb la funció poligamma:

${\psi }^{(m)}(z)=(-1{)}^{m+1}m!\zeta (m+1,z).$

Per a nombres enters negatius −n els valors estan relacionats amb els polinomis de Bernoulli:

$\zeta (-n,x)=-\frac{B_{n+1}(x)}{n+1}.$

La funció zeta de Barnes generalitza la funció zeta de Hurwitz.

El transcendent de Lerch generalitza la funció zeta de Hurwitz:

$\mathrm{\Phi }(z,s,q)=\sum _{k=0}^{\mathrm{\infty }}\frac{z^k}{(k+q{)}^s}$

i per tant

$\zeta (s,q)=\mathrm{\Phi }(1,s,q).$

Funció hipergeomètrica

$\zeta (s,a)=a^{-s}\cdot {}_{s+1}{F}_s(1,a_1,a_2,\dots a_s;a_1+1,a_2+1,\dots a_s+1;1)$ on $a_1=a_2=\dots =a_s=a\text{ i }a\notin \mathbb{N}\text{ i }s\in {\mathbb{N}}^{+}.$

Funció G de Meijer

$\zeta (s,a)=G{}_{s+1,s+1}^{1,s+1}(-1\left|\begin{array}{c}0,1-a,\dots ,1-a\\ 0,-a,\dots ,-a\end{array}\right)s\in {\mathbb{N}}^{+}.$

Bibliografia

• Plantilla:Ref-llibre
• Plantilla:Ref-llibre
• Plantilla:Ref-publicació
• Plantilla:Ref-publicació Plantilla:Webarchive
• Plantilla:Ref-web