Funció digamma

Representació de la funció digamma $\psi (x)$ restringit als reals.

Representació en color de la funció digamma, $\psi (z)$, en una regió rectangular del pla complex

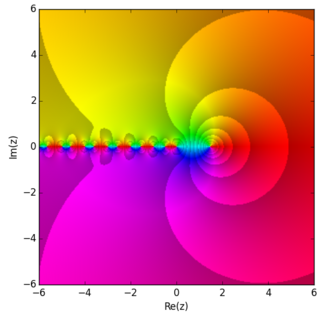
En matemàtiques, la funció digamma es defineix com la derivada logarítmica de la funció gamma:

$\psi (x)=\frac{d}{dx}\ln (\mathrm{\Gamma }(x))=\frac{{\mathrm{\Gamma }}^{\prime }(x)}{\mathrm{\Gamma }(x)}.$

És la primera de les funcions poligamma.

La funció digamma sovint es denota com a ${\psi }_0(x)$, ${\psi }^{(0)}(x)$ o Plantilla:Math (la forma en majúscula de la consonant grega arcaica digamma, que significa doble gamma).

Història i notacions

Seguint el treball d'Euler sobre la funció gamma, James Stirling va introduir la funció digamma en 1730, denotant-la Ϝ, la lletra grega digamma (majúscula). Més tard va ser estudiada per Legendre, Poisson i Gauss al voltant de 1810; la convergència de la sèrie de Stirling per a aquesta funció va ser demostrada per Stern en 1847.

Actualment se sol denotar amb la lletra $\psi$ (psi minúscula).

Motivació

Considerant la funció gamma com una generalització formal del factorial (més precisament, $\mathrm{\Gamma }(x)=1\times 2\times \dots \times (x-1)$), es pot deduir de la mateixa manera que de forma formal, utilitzant les propietats de la derivada logarítmica, obtenim

$\psi (z)=\frac{{\mathrm{\Gamma }}^{\prime }(z)}{\mathrm{\Gamma }(z)}=1+1/2+1/3+\dots +1/(z-1)=H_{z-1},$

on $H_n$ és el n-èsim nombre harmònic.

Així, la funció digamma podria definir una generalització dels nombres harmònics als complexos. Una fórmula exacta per a ${\psi }_{(n)}$, gairebé confirmant el càlcul anterior, s'obté de forma més baixa estrictament per a $n$ enter.

Propietats

La funció digamma és una funció meromorfa definida en tot el pla complex privat dels enters negatius.

La definició d'Euler de la funció gamma en forma integral mostra que per a qualsevol nombre complex $z$ d'una part real estrictament positiva,

$\psi (z)=\frac{\underset{0}{\overset{\mathrm{\infty }}{\int }}{y}^{z-1}\ln y{\mathrm{e}}^{-y}\mathrm{d}y}{\underset{0}{\overset{\mathrm{\infty }}{\int }}{y}^{z-1}{\mathrm{e}}^{-y}\mathrm{d}y}.$

Així,

$\psi (1)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\ln y{\mathrm{e}}^{-y}\mathrm{d}y=-\gamma$, on $\gamma =0,57721566490153$ és la constant d'Euler-Mascheroni.

D'altra banda, $\mathrm{\Gamma }(z+1)=z\mathrm{\Gamma }(z)$ per tant tenim (al derivar) la relació de recurrència

$\psi (z+1)=\psi (z)+\frac{1}{z};$

de fet, el teorema de Bohr-Mollerup mostra que la funció digamma és l'única solució de l'equació funcional

$F(x+1)=F(x)+\frac{1}{x}$

que és monòtona sobre Plantilla:Math i que verifica $F(1)=-\gamma$

A partir d'això, es dedueix que la funció digamma d'un enter $n>0$, sovint denotat també ${\psi }_0(n)$ o fins i tot ${\psi }^{(0)}(n)$, està connectada als nombres harmònics per

$\frac{\underset{0}{\overset{\mathrm{\infty }}{\int }}{y}^{n-1}\ln y{\mathrm{e}}^{-y}\mathrm{d}y}{(n-1)!}=\psi (n)=H_{n-1}-\gamma$

on $H_{n-1}=1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n-1}$ és el (n – 1)-ésim nombre harmònic.

La funció digamma també satisfà una fórmula de reflexió similar a la de la funció gamma: per a qualsevol nombre complex $z$ la part real del qual sigui estrictament entre $0$ i $1$,

$\psi (1-z)-\psi (z)=\pi \cot \left(\pi z\right).$

Existeixen altres representacions per integrals. Per tant, si la part real de $z$ és positiva, tenim:

$\psi (z)=\underset{0}{\overset{\mathrm{\infty }}{\int }}(\frac{{\mathrm{e}}^{-t}}{t}-\frac{{\mathrm{e}}^{-zt}}{1-{\mathrm{e}}^{-t}})\mathrm{d}t,$

que també podem escriure

$\psi (s+1)=-\gamma +\underset{0}{\overset{1}{\int }}\frac{1-x^s}{1-x}\mathrm{d}x.$

Relació amb els nombres harmònics

La funció gamma obeeix a l'equació

$\mathrm{\Gamma }(z+1)=z\mathrm{\Gamma }(z).$

Prenent la derivada pel que fa a $z$ dona:

${\mathrm{\Gamma }}^{\prime }(z+1)=z{\mathrm{\Gamma }}^{\prime }(z)+\mathrm{\Gamma }(z)$

Dividint per $\mathrm{\Gamma }(z+1)$, o l'equivalent $z\mathrm{\Gamma }(z)$, dona:

$\frac{{\mathrm{\Gamma }}^{\prime }(z+1)}{\mathrm{\Gamma }(z+1)}=\frac{{\mathrm{\Gamma }}^{\prime }(z)}{\mathrm{\Gamma }(z)}+\frac{1}{z}$

o:

$\psi (z+1)=\psi (z)+\frac{1}{z}$

Atès que els nombres harmònics es defineixen com

$H_n=\sum _{k=1}^n\frac{1}{k}$

la funció digamma està relacionada amb ells per:

$\psi (n)=H_{n-1}-\gamma$

on $H_n$ és el n-èsim nombre harmònic, i $\gamma$ és la constant d'Euler-Mascheroni. Per als valors de mig enters, es pot expressar com a

$\psi (n+\frac{1}{2})=-\gamma -2\ln 2+\sum _{k=1}^n\frac{2}{2k-1}$

Representació en integrals

Si la part real de $x$ és positiva, la funció de digamma té la següent representació integral

$\psi (x)=\underset{0}{\overset{\mathrm{\infty }}{\int }}(\frac{e^{-t}}{t}-\frac{e^{-xt}}{1-e^{-t}})dt.$

Això també es pot escriure com

$\psi (s+1)=-\gamma +\underset{0}{\overset{1}{\int }}\left(\frac{1-x^s}{1-x}\right)dx$

que es dedueix de la fórmula integral de Leonhard Euler per als nombres harmònics.

Representació en producte infinit

La funció $\psi (z)/\mathrm{\Gamma }(z)$ és una funció entera, i pot ser representada per un producte infinit

$\frac{\psi (z)}{\mathrm{\Gamma }(z)}=-e^{2\gamma z}\prod _{k=0}^{\mathrm{\infty }}(1-\frac{z}{x_k})e^{\frac{z}{x_k}}.$

Aquí $x_k$ és el k-èsim zero $\psi$ (vegeu més avall), i $\gamma$ és la constant d'Euler-Mascheroni.

Representació en sèries

La funció digamma es pot calcular al pla complex fora dels enters negatius (Abramowitz i Stegun 6.3.16), utilitzant

$\psi (z+1)=-\gamma +\sum _{n=1}^{\mathrm{\infty }}\frac{z}{n(n+z)}z\ne -1,-2,-3,\dots$

o

$\psi (z)=-\gamma +\sum _{n=0}^{\mathrm{\infty }}\frac{z-1}{(n+1)(n+z)}=-\gamma +\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{n+1}-\frac{1}{n+z})z\ne 0,-1,-2,-3,\dots$

Això es pot utilitzar per avaluar sumes infinites de funcions racionals, és a dir,

$\sum _{n=0}^{\mathrm{\infty }}{u}_n=\sum _{n=0}^{\mathrm{\infty }}\frac{p(n)}{q(n)},$

on $p(n)$ i $q(n)$ són polinomis de $n$.

Realitzant una fracció parcial $u_n$ en el camp complex, en el cas en què totes les arrels de $q(n)$ siguin arrels simples, llavors

$u_n=\frac{p(n)}{q(n)}=\sum _{k=1}^m\frac{a_k}{n+b_k}.$

Per a la convergència de la sèrie,

$\underset{n\to \mathrm{\infty }}{\lim }n{u}_n=0,$

en cas contrari la sèrie serà més gran que la sèrie harmònica i, per tant, divergirà. Per tant

$\sum _{k=1}^m{a}_k=0,$

i

$\begin{array}{cc}\sum _{n=0}^{\mathrm{\infty }}{u}_n& =\sum _{n=0}^{\mathrm{\infty }}\sum _{k=1}^m\frac{a_k}{n+b_k}\\ & =\sum _{n=0}^{\mathrm{\infty }}\sum _{k=1}^m{a}_k(\frac{1}{n+b_k}-\frac{1}{n+1})\\ & =\sum _{k=1}^m\left(a_k\sum _{n=0}^{\mathrm{\infty }}(\frac{1}{n+b_k}-\frac{1}{n+1})\right)\\ & =-\sum _{k=1}^m{a}_k(\psi (b_k)+\gamma )\\ & =-\sum _{k=1}^m{a}_k\psi (b_k).\end{array}$

Amb el desenvolupament de la sèrie de funció poligamma de rang superior, es pot donar una fórmula generalitzada com

$\sum _{n=0}^{\mathrm{\infty }}{u}_n=\sum _{n=0}^{\mathrm{\infty }}\sum _{k=1}^m\frac{a_k}{(n+b_k{)}^{r_k}}=\sum _{k=1}^m\frac{(-1{)}^{r_k}}{(r_k-1)!}{a}_k{\psi }^{r_k-1}(b_k),$

sempre que la sèrie de l'esquerra convergeixi.

Representació en sèrie de Taylor

La funció digamma té una sèrie zeta racional, donada per la sèrie de Taylor en $z=1$. Aquesta és

$\psi (z+1)=-\gamma -\sum _{k=1}^{\mathrm{\infty }}\zeta (k+1)(-z{)}^k,$

que convergeix per a $\left|z\right|<1$. Aquesta, $\zeta (n)$ és la funció zeta de Riemann. Aquesta sèrie es deriva fàcilment de la corresponent sèrie de Taylor per a la funció zeta de Hurwitz.

Representació en sèrie de Newton

La sèrie de Newton per a la digamma es desprèn de la fórmula de la integral d'Euler:

$\psi (s+1)=-\gamma -\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^k}{k}(\genfrac{}{}{0ex}{}{s}{k})$

on $(\genfrac{}{}{0ex}{}{s}{k})$és el coeficient binomial: $(\genfrac{}{}{0ex}{}{s}{k})=\frac{s(s-1)(s-2)\cdots (s-k+1)}{k!}$.

Fórmula de reflexió

La funció digamma satisfà una fórmula de reflexió similar a la de la funció gamma:

$\psi (1-x)-\psi (x)=\pi \cot \pi x$

Fórmula de recurrència

La funció digamma satisfà la relació de recurrència

$\psi (x+1)=\psi (x)+\frac{1}{x}.$

Per tant, es pot dir «telescopi» $\frac{1}{x}$, quan

$\mathrm{\Delta }[\psi ](x)=\frac{1}{x}$

on $\mathrm{\Delta }$ és l'operador de diferència progressiva. Això satisfà la relació de recurrència d'una suma parcial de la sèrie harmònica, el que implica la fórmula

$\psi (n)=H_{n-1}-\gamma$

on $\gamma$ és la constant d'Euler-Mascheroni.

En general, s'obté

$\psi (x+1)=-\gamma +\sum _{k=1}^{\mathrm{\infty }}(\frac{1}{k}-\frac{1}{x+k}).$

En realitat, $\psi$ és l'única solució de l'equació funcional

$F(x+1)=F(x)+\frac{1}{x}$

que és monòtona en Plantilla:Math i satisfà $F(1)=-\gamma$. Aquest fet es dedueix de la unicitat de la funció $\mathrm{\Gamma }$ donada la seva equació de recurrència i la restricció de convexitat. Això implica l'equació de la diferència útil:

$\psi (x+N)-\psi (x)=\sum _{k=0}^{N-1}\frac{1}{x+k}$

Algunes sumes finites que inclouen la funció digamma

Existeixen nombroses fórmules de sumes finites per a la funció digamma. Algunes fórmules de sumes finites bàsiques són:

$\sum _{r=1}^m\psi \left(\frac{r}{m}\right)=-m(\gamma +\ln m),$

$\sum _{r=1}^m\psi \left(\frac{r}{m}\right)\cdot \exp \frac{2\pi rki}{m}=m\ln (1-\exp \frac{2\pi ki}{m}),k\in \mathbb{Z},m\in \mathbb{N},k\ne m.$

$\sum _{r=1}^{m-1}\psi \left(\frac{r}{m}\right)\cdot \cos \frac{2\pi rk}{m}=m\ln (2\sin \frac{k\pi }{m})+\gamma ,k=1,2,\dots ,m-1$

$\sum _{r=1}^{m-1}\psi \left(\frac{r}{m}\right)\cdot \sin \frac{2\pi rk}{m}=\frac{\pi }{2}(2k-m),k=1,2,\dots ,m-1$

que es deuen a Gauss. Altres fórmules, més complexes, són

$\sum _{r=0}^{m-1}\psi \left(\frac{2r+1}{2m}\right)\cdot \cos \frac{(2r+1)k\pi }{m}=m\ln (\tan \frac{\pi k}{2m}),k=1,2,\dots ,m-1$

$\sum _{r=0}^{m-1}\psi \left(\frac{2r+1}{2m}\right)\cdot \sin \frac{(2r+1)k\pi }{m}=-\frac{\pi m}{2},k=1,2,\dots ,m-1$

$\sum _{r=1}^{m-1}\psi \left(\frac{r}{m}\right)\cdot \cot \frac{\pi r}{m}=-\frac{\pi (m-1)(m-2)}{6}$

$\sum _{r=1}^{m-1}\psi \left(\frac{r}{m}\right)\cdot \frac{r}{m}=-\frac{\gamma }{2}(m-1)-\frac{m}{2}\ln m-\frac{\pi }{2}\sum _{r=1}^{m-1}\frac{r}{m}\cdot \cot \frac{\pi r}{m}$

$\sum _{r=1}^{m-1}\psi \left(\frac{r}{m}\right)\cdot \cos \frac{(2\ell +1)\pi r}{m}=-\frac{\pi }{m}\sum _{r=1}^{m-1}\frac{r\cdot \sin \frac{2\pi r}{m}}{\cos \frac{2\pi r}{m}-\cos \frac{(2\ell +1)\pi }{m}},\ell \in \mathbb{Z}$

$\sum _{r=1}^{m-1}\psi \left(\frac{r}{m}\right)\cdot \sin \frac{(2\ell +1)\pi r}{m}=-(\gamma +\ln 2m)\cot \frac{(2\ell +1)\pi }{2m}+\sin \frac{(2\ell +1)\pi }{m}\sum _{r=1}^{m-1}\frac{\ln \sin \frac{\pi r}{m}}{\cos \frac{2\pi r}{m}-\cos \frac{(2\ell +1)\pi }{m}},\ell \in \mathbb{Z}$

$\sum _{r=1}^{m-1}{\psi }^2\left(\frac{r}{m}\right)=(m-1){\gamma }^2+m(2\gamma +\ln 4m)\ln m-m(m-1){\ln }^{2}2+\frac{{\pi }^2(m^2-3m+2)}{12}+m\sum _{\ell =1}^{m-1}{\ln }^2\sin \frac{\pi \ell }{m}$

es deuen a treballs de certs autors moderns (vegeu per exemple Appendix B de Blagouchine (2014)).

Teorema de la digamma de Gauss

Per als nombres enters positius $r$ i $m$ ($r<m$), la funció digamma es pot expressar en termes de la constant d'Euler-Mascheroni i un nombre finit de funcions elementals

$\psi \left(\frac{r}{m}\right)=-\gamma -\ln (2m)-\frac{\pi }{2}\cot \left(\frac{r\pi }{m}\right)+2\sum _{n=1}^{\lfloor \frac{m-1}{2}\rfloor }\cos \left(\frac{2\pi nr}{m}\right)\ln \sin \left(\frac{\pi n}{m}\right)$

que es manté, per raó de la seva equació de recurrència, per a tots els arguments racionals.

Càlcul aproximat

Segons la fórmula d'Euler-Maclaurin aplicada a

$\sum _{n=1}^x\frac{1}{n}$

la funció digamma per a $x$, un nombre real, es pot aproximar per

$\psi (x)\approx \ln (x)-\frac{1}{2x}-\frac{1}{12x^2}+\frac{1}{120x^4}-\frac{1}{252x^6}+\frac{1}{240x^8}-\frac{5}{660x^{10}}+\frac{691}{32760x^{12}}-\frac{1}{12x^{14}}$

que és el començament del desenvolupament asimptòtic de $\psi (x)$. La sèrie asimptòtica completa d'aquests desenvolupaments és

$\psi (x)\sim \ln (x)-\frac{1}{2x}+\sum _{n=1}^{\mathrm{\infty }}\frac{\zeta (1-2n)}{x^{2n}}=\ln (x)-\frac{1}{2x}-\sum _{n=1}^{\mathrm{\infty }}\frac{B_{2n}}{2n{x}^{2n}}$

on $B_k$ és el k-ésim nombre de Bernoulli i $\zeta$ és la funció zeta de Riemann. Encara que la suma infinita no convergeix per a cap $x$, aquest desenvolupament es fa més precisa per a valors més grans de $x$ i qualsevol suma parcial finita extreta de la sèrie completa. Per calcular $\psi (x)$ per $x$ petit, la relació de recurrència és

$\psi (x+1)=\frac{1}{x}+\psi (x)$

es pot utilitzar per canviar el valor de $x$ a un valor superior. Beal suggereix utilitzar la recurrència anterior per canviar $x$ a un valor superior a $6$ i aplicar l'anterior desenvolupament amb els termes anteriors $x^{14}$ tallats, el que produeix «més que suficient precisió» (almenys 12 dígits, excepte prop del zero).

Com $x$ tendeix cap a l'infinit, $\psi (x)$ s'aproxima arbitràriament tant a $\ln (x-1/2)$ com a $\ln x$. Si es baixa de $x+1$ a $x$, $\psi$ disminueix en $\frac{1}{x}$, $\ln (x-1/2)$ disminueix amb $\frac{\ln (x+1/2)}{\ln (x-1/2)}$, que és més que $\frac{1}{x}$, i $\ln x$ disminueix amb $\ln (1-1/x)$, que és inferior a $\frac{1}{x}$. D'això veiem que per a qualsevol positiva $x$ major que $\frac{1}{2}$,

$\psi (x)\in (\ln (x-\frac{1}{2}),\ln x)$

o, per a qualsevol $x$ positiva,

$\exp \psi (x)\in (x-\frac{1}{2},x).$

L'exponencial $\exp \psi (x)$ és aproximadament $x-1/2$ al llarg de $x$, però s'acosta més a $x$ quan $x$ és més petit, aproximant-se a $0$ en $x=0$.

Per $x<1$, podem calcular límits en funció del fet que entre $1$ i $2$, $\psi (x)\in [-\gamma ,1-\gamma ]$, d'aquesta manera

$\psi (x)\in (-\frac{1}{x}-\gamma ,1-\frac{1}{x}-\gamma ),x\in (0,1)$

o

$\exp \psi (x)\in (\exp (-\frac{1}{x}-\gamma ),e\exp (-\frac{1}{x}-\gamma )).$

A partir de la sèrie asimptòtica anterior per $\psi$, es pot derivar una sèrie asimptòtica per $\exp (-\psi (x))$. La sèrie coincideix bé amb el comportament general, és a dir, es comporta de forma asimptòtica com per grans arguments, i també té un zero de multiplicitat il·limitada a l'origen.

$\frac{1}{\exp \psi (x)}\sim \frac{1}{x}+\frac{1}{2\cdot x^2}+\frac{5}{4\cdot 3!\cdot x^3}+\frac{3}{2\cdot 4!\cdot x^4}+\frac{47}{48\cdot 5!\cdot x^5}-\frac{5}{16\cdot 6!\cdot x^6}+\cdots$

Això és similar al desenvolupament de la sèrie de Taylor $(-\psi (1/y))$ en $y=0$, però no convergeix. (La funció no és analítica a l'infinit). Existeix una sèrie similar per a $\exp \psi (x)$ que comença amb $\exp \psi (x)\sim x-\frac{1}{2}.$

Si es calcula la sèrie asimptòtica per a $\exp \psi (x+1/2)$, resulta que no hi ha potències senars de $x$ (no hi ha terme $x^{-1}$). Això condueix al següent desenvolupament asimptòtic, que estalvia computar termes d'ordre parell.

$\exp \psi (x+\frac{1}{2})\sim x+\frac{1}{4!\cdot x}-\frac{37}{8\cdot 6!\cdot x^3}+\frac{10313}{72\cdot 8!\cdot x^5}-\frac{5509121}{384\cdot 10!\cdot x^7}+\cdots$

Valors especials

La funció digamma té valors en forma tancada per a nombres racionals, com a resultat del teorema de la digamma de Gauss. Alguns es detallen a continuació:

$\begin{array}{cc}\psi (1)& =-\gamma \\ \psi (2)& =H_1-\gamma =1-\gamma \\ \psi (3)& =H_2-\gamma =\frac{3}{2}-\gamma \\ \psi (4)& =H_3-\gamma =\frac{11}{6}-\gamma \\ \psi \left(\frac{1}{2}\right)& =-2\ln 2-\gamma =\frac{1}{\sqrt{\pi }}\underset{0}{\overset{\mathrm{\infty }}{\int }}{y}^{-1/2}\ln y{\mathrm{e}}^{-y}\mathrm{d}y\\ \psi \left(\frac{1}{3}\right)& =-\frac{\pi }{2\sqrt{3}}-\frac{3\ln 3}{2}-\gamma \\ \psi \left(\frac{1}{4}\right)& =-\frac{\pi }{2}-3\ln 2-\gamma \\ \psi \left(\frac{1}{6}\right)& =-\frac{\pi \sqrt{3}}{2}-2\ln 2-\frac{3\ln 3}{2}-\gamma \\ \psi \left(\frac{1}{8}\right)& =-\frac{\pi }{2}-4\ln 2-\frac{\pi +\ln (2+\sqrt{2})-\ln (2-\sqrt{2})}{\sqrt{2}}-\gamma .\end{array}$

A més, per la representació de la sèrie, es pot deduir fàcilment que la unitat imaginària,

$\begin{array}{cc}\mathrm{Re}\psi (i)& =-\gamma -\sum _{n=0}^{\mathrm{\infty }}\frac{n-1}{n^3+n^2+n+1},\\ [8px]\mathrm{Im}\psi (i)& =\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n^2+1}=\frac{1}{2}+\frac{\pi }{2}\coth \pi .\end{array}$

Arrels de la funció digamma

Les arrels de la funció digamma són els punts de la cadira de muntar de la funció gamma de valors complexos. Així, es troben tots a l'eix real. L'únic en l'eix real positiu és l'únic valor mínim de la funció gamma de valors reals en Plantilla:Math en x₀ = 1,461632144968 ... Tots els altres tenen lloc entre els pols de l'eix negatiu:

$\begin{array}{cc}{x}_1& =-0.504083008\dots ,\\ x_2& =-1.573498473\dots ,\\ x_3& =-2.610720868\dots ,\\ x_4& =-3.635293366\dots ,\\ & ⋮\end{array}$

Al voltant de 1881, Charles Hermite va observar que

$x_n=-n+\frac{1}{\ln n}+O\left(\frac{1}{(\ln n{)}^2}\right)$

es manté asimptòticament. Es proporciona una millor aproximació de la ubicació de les arrels

$x_n\approx -n+\frac{1}{\pi }\arctan \left(\frac{\pi }{\ln n}\right)n\ge 2$

i utilitzant un terme addicional, es torna encara millor

$x_n\approx -n+\frac{1}{\pi }\arctan \left(\frac{\pi }{\ln n+\frac{1}{8n}}\right)n\ge 1$

que tant surt en la fórmula de reflexió a través de

$0=\psi (1-x_n)=\psi (x_n)+\frac{\pi }{\tan \pi x_n}$

i substituint $\psi (xn)$ per al seu desenvolupament asimptòtic no convergent. El segon terme correcte d'aquest desenvolupament és $1/2n$, funciona bé per aproximar-se a les arrels amb un petit $n$.

Es pot donar una altra millora amb el polinomi d'Hermite:

$x_n=-n+\frac{1}{\log n}-\frac{1}{2n(\log n{)}^2}+O\left(\frac{1}{n^2(\log n{)}^2}\right).$

Pel que fa als zeros, István Mező i Michael Hoffman han demostrat recentment les següents identitats de suma infinita:

$\begin{array}{cc}\sum _{n=0}^{\mathrm{\infty }}\frac{1}{x_n^2}& ={\gamma }^2+\frac{{\pi }^2}{2},\\ \sum _{n=0}^{\mathrm{\infty }}\frac{1}{x_n^3}& =-4\zeta (3)-{\gamma }^3-\frac{\gamma {\pi }^2}{2},\\ \sum _{n=0}^{\mathrm{\infty }}\frac{1}{x_n^4}& ={\gamma }^4+\frac{{\pi }^4}{9}+\frac{2}{3}{\gamma }^2{\pi }^2+4\gamma \zeta (3).\end{array}$

En general, la funció

$Z(k)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{x_n^k}$

es pot determinar i és estudiat en detall pels autors citats.

Els resultats següents

$\begin{array}{cc}\sum _{n=0}^{\mathrm{\infty }}\frac{1}{x_n^2+x_n}& =-2,\\ \sum _{n=0}^{\mathrm{\infty }}\frac{1}{x_n^2-x_n}& =\gamma +\frac{{\pi }^2}{6\gamma }\end{array}$

també és veritat.

Aquí $\gamma$ és la constant d'Euler-Mascheroni.

Regularització

La funció digamma apareix en la regularització d'integrals divergents

$\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{dx}{x+a},$

aquesta integral pot ser aproximada per una sèrie harmònica general divergent, però es pot adjuntar el següent valor a la sèrie

$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n+a}=-\psi (a).$

Vegeu també

• Funció gamma.
• Funció trigamma (no confondre amb la funció gamma triple).
• Funció poligamma (no confondre amb la funció gamma múltiple).

Enllaços externs

• $\psi (1/2)$ Plantilla:OEIS
• $\psi (1/3)$ Plantilla:OEIS
• Desenvolupament de Txebixov de la funció digamma en Plantilla:Ref-publicació