Nombre e

El gràfic Plantilla:Nowrap, i e és el nombre que fa l'àrea igual a 1.

La constant matemàtica e és la base dels logaritmes naturals, és l'únic nombre el logaritme natural del qual és 1. És considerat el nombre per excel·lència del càlcul de la mateixa manera que el nombre $\pi$  ho és de la geometria. El nombre e s'anomena a vegades constant d'Euler, en honor del matemàtic suís Leonhard Euler i també constant de Napier, en honor del matemàtic escocès John Napier que va introduir els logaritmes.

El número e té una importància eminent en matemàtiques al costat de 0, 1, [[Nombre_π|Plantilla:Math]] i [[Nombre imaginari|Plantilla:Math]]. Els cinc apareixen en una formulació de la identitat d'Euler i tenen un paper important i recurrent en les matemàtiques. Igual que la constant π, e és irracional (és a dir, no es pot representar com una proporció de nombres enters) i transcendent (és a dir, no és una arrel de cap polinomi diferent de zero amb coeficients racionals). Les primeres xifres de la seva expressió decimal il·limitada són 2,7182818284590. És un nombre present en múltiples camps de la ciència i la tècnica. Intervé, per exemple en el càlcul de la velocitat de buidatge d'un dipòsit d'aigua, en el gir d'un penell enfront d'una ràfega de vent o el moviment del sistema amortidor d'un automòbil.

Definició

El nombre e es defineix com el límit de la successió $n\mapsto {(1+\frac{1}{n})}^n$. Aquest límit existeix, ja que la successió és creixent i limitada per sobre.

$e=\underset{n\to \mathrm{\infty }}{\lim }{(1+\frac{1}{n})}^n$

Aquesta expressió del nombre e apareix en l'estudi de l'interès compost. El nombre e apareix en múltiples camps de les matemàtiques, des de la teoria de la probabilitat a l'anàlisi complexa. El seu valor aproximat per truncament als 50 decimals és 2,71828182845904523536028747135266249775724709369995

El nombre e es pot definir també mitjançant la sèrie infinita

$e=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{n!}=\frac{1}{0!}+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots$

on n! és el factorial de n. Aquesta sèrie convergeix puix que hom té

$1+1+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots \le 1+1+\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\cdots =3,$

és a dir, el desenvolupament en sèrie de e és majorat mitjançant una sèrie geomètrica que és convergent perquè té una raó igual a 1/2.

Finalment, es pot considerar e com a l'única solució positiva x de l'equació integral

$\underset{1}{\overset{x}{\int }}\frac{1}{t}dt=1.$

Es pot demostrar que aquestes definicions són equivalents.

La funció exponencial $x⟼e^x$és important ja que és l'única (a menys de multiplicació per constants) funció que és igual a la seva derivada, i s'usa habitualment per a modelitzar processos de creixement o decreixement.

La fracció contínua de e conté una estructura interessant, com es mostra a continuació:

$e=[2;1,2,1,1,4,1,1,6,1,1,8,1,1,10,1,1,12...]$

Història

Les primeres referències a la constant es van publicar el 1618 a la taula d'un apèndix d'un treball sobre logaritmes de John Napier. Tanmateix no contenia la constant en si, sinó simplement una llista de logaritmes calculats a partir de la constant. Se suposa que la taula va ser escrita per William Oughtred. El propi descobriment de la constant s’acredita a Jacob Bernoulli el 1683, que va intentar trobar el valor de la següent expressió (que és igual a e):

$\underset{n\to \mathrm{\infty }}{\lim }{(1+\frac{1}{n})}^n.$

El primer ús conegut de la constant, representat per la lletra b, fou en correspondència de Gottfried Leibniz a Christiaan Huygens el 1690 i el 1691. Leonhard Euler va introduir la lletra e com a base per als logaritmes naturals, escrivint en una carta a Christian Goldbach el 25 de novembre de 1731. Euler va començar a utilitzar la lletra e per a la constant el 1727 o el 1728, en un document inèdit sobre les forces explosives en canons, mentre que la primera aparició dPlantilla:'e en una publicació va ser a Mechanica, sive motus scientia analytica exposita (1736).

Propietats

Càlcul

Com en la motivació, la funció exponencial Plantilla:Math és important en part perquè és l'única funció (llevat de multiplicació per una constant Plantilla:Mvar) que és igual a la seva pròpia derivada:

$\frac{d}{dx}K{e}^x=K{e}^x,$

i per tant també és igual a la seva pròpia primitiva:

$\int K{e}^{x}dx=K{e}^x+C.$

Equivalentment, la família de funcions

$y(x)=K{e}^x$

on Plantilla:Mvar és un nombre complex qualsevol, és la solució completa a l'equació diferencial

$y^{\prime }=y.$

Desigualtats

Funcions exponencials Plantilla:Math i Plantilla:Math intersecten la gràfica de Plantilla:Math, respectivament, a Plantilla:Math i a Plantilla:Math. El nombre Plantilla:Math és l'única base tal que Plantilla:Math intersecta només a Plantilla:Math. Es pot inferir que Plantilla:Math es troba entre el 2 i el 4.

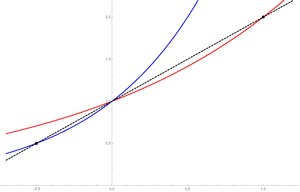
El nombre Plantilla:Math és l'únic nombre real tal que

${(1+\frac{1}{x})}^x<e<{(1+\frac{1}{x})}^{x+1}$

per tot Plantilla:Math positiu.

També existeix la següent desigualtat

$e^x\ge x+1$

per tot Plantilla:Math real, i hi ha igualtat si i només si Plantilla:Math. A més, Plantilla:Math és l'única base de l'exponencial per la qual la desigualtat Plantilla:Math és vàlida per tot Plantilla:Math. Això és un cas límit de la desigualtat de Bernoulli.

Funcions de tipus exponencial

El màxim global de Plantilla:Math Plantilla:Nowrap

El problema de Steiner consisteix a trobar el màxim global de la funció

$f(x)=x^{\frac{1}{x}}.$

Aquest màxim es dóns precisament a Plantilla:Math. (Es pot comprovar que la derivada de Plantilla:Math és zero només per aquest valor de  Plantilla:Mvar.)

Similarment, Plantilla:Math és quan hi ha el mínim global de la funció

$f(x)=x^x.$

La tetració infinita

$x^{x^{x^{{\cdot }^{{\cdot }^{\cdot }}}}}$ o ${}^{\mathrm{\infty }}x$

congergeix si i només si Plantilla:Math, demostrat per un teorema de Leonhard Euler.

Teoria de nombres

El nombre real Plantilla:Mvar és irracional. Euler ho va demostrar observant que la seva expansió en fracció contínua no acaba mai. (Vegi's també la demostració que e és irracional de Fourier.)

A més, a partir del teorema de Lindemann-Weierstrass, Plantilla:Mvar és transcendent, en el sentit que no és solució de cap equació polinomial no-sero amb coeficients racionals. Va ser el primer nombre del qual es va demostrar aquesta propietat sense haver estat específicament demostrat amb aquest propòsit (compari's amb el nombre de Liouville); la demostració va ser a càrrec de Charles Hermite l'any 1873.

S'ha conjecturat que Plantilla:Mvar és un normal, en el sentit que quan Plantilla:Math s'expressa en qualsevol base els possibles dígits en aquella base estan distribuïts uniformement (apareixen en igual probabilitat en qualsevol seqüència d'una longitud donada).

S'ha conjecturat que Plantilla:Mvar no és un període de Kontsevich-Zagier.

Nombres complexos

Es pot escriure la funció exponencial Plantilla:Math com una expansió en sèrie de Taylor

$e^x=1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{x^n}{n!}.$

Com que la sèrie és convergent per tot valor complex de Plantilla:Mvar, s'utilitza habitualment per estendre la definició de Plantilla:Math als nombres complexos. Això, juntament amb la sèrie de Taylor per al [[funcions trigonomètriques|Plantilla:Math i Plantilla:Math]], permet derivar la fórmula d'Euler:

$e^{ix}=\cos x+i\sin x,$

que és vàlid per tot valor complex de Plantilla:Math. El cas particular amb Plantilla:Math és la identitat d'Euler:

$e^{i\pi }+1=0,$

de la qual segueix que, en la branca principal del logaritme,

$\ln (-1)=i\pi .$

A més, utilitzant les lleis de l'exponenciació,

$(\cos x+i\sin x{)}^n={\left(e^{ix}\right)}^n=e^{inx}=\cos (nx)+i\sin (nx),$

que és la fórmula de De Moivre.

Es poden deduir les expressions de Plantilla:Math i Plantilla:Math en termes de la funció exponencial a partir de la sèrie de Taylor:

$\cos x=\frac{e^{ix}+e^{-ix}}{2},\sin x=\frac{e^{ix}-e^{-ix}}{2i}.$

L'expressió

$\cos x+i\sin x$

és sovint abreviada com Plantilla:Math.

Dígits coneguts

El nombre dels dígits coneguts de Plantilla:Mvar ha augmentat substancialment durant les darreres dècades. Això es deu tant a la millora dels ordinadors així com la dels algorismes.

Nombre de dígits decimals coneguts de Plantilla:Mvar

Data	Dígits decimals	Càlcul fet per
1690	1	Jacob Bernoulli
1714	13	Roger Cotes
1748	23	Leonhard Euler
1853	137	William Shanks
1871	205	William Shanks
1884	346	J. Marcus Boorman
1949	2,010	John von Neumann (a l'ENIAC)
1961	100,265	Daniel Shanks i John Wrench
1978	116,000	Steve Wozniak amb l'Apple II

Des de 2010, la proliferació dels ordinadors de taula d'alta velocitat ha permès a aficionats calcular trilions de dígits de Plantilla:Mvar en quantitats de temps acceptables. El 5 de desembre de 2020, es va fer un càlcul de rècord, trobant 31 415 926 535 897 (aproximadament Plantilla:Mvar × 10¹³) dígits de Plantilla:Mvar.

Identitat d'Euler

Plantilla:Article principal La següent expressió, la identitat d'Euler, que relaciona les cinc constants més importants en matemàtiques, va ser descoberta per Leonhard Euler:

$e^{i\pi }+1=0$

Aquesta és un cas particular (amb x = 0 i y = π) de la fórmula d'Euler:

$e^{x+i\cdot y}=e^x\cdot (\cos y+i\cdot \sin y)$

vàlida per a tot $x,y\in ℝ$ (i de fet per a tot $x,y\in ℂ$).

Asímptotes

El nombre e surt de manera natural en diferents problemes que involucren les asímptotes. N'és un exemple la fórmula de Stirling que es fa servir per a l'anàlisi asimptòtica de la funció factorial, on els dos nombres e i π es troben involucrats:

$n!\sim \sqrt{2\pi n}{\left(\frac{n}{e}\right)}^n.$

Una conseqüència particular és:

$e=\underset{n\to \mathrm{\infty }}{\lim }\frac{n}{\sqrt[n]{n!}}$.

Implementació en informàtica

Es pot calcular una aproximació del nombre e amb n termes de la seqüència de Taylor citada. En C++ tenim un codi com el següent:

#include <iostream>
using namespace std;

double aproxima_e(int n) {
 //funció que aproxima el nombre e amb la seqüència de taylor:
 // suma 1/fact(i) des de i=0 fins n
 //no cal fer servir la funció factorial en cada denominador.
 if(n == 0) return 0;
 double facti = 1; //ini a 1: factorial(0). necessitem que sigui double per evitar errors de sobreeiximent
 double s = 1;
 for(int i = 1; i < n; ++i) {
 facti *= i; 
 s += 1/double(facti); 
 }

 return s;
}

int main() {
 cout.setf(ios::fixed);
 cout.precision(10);

 int n;
 while(cin >> n) {
 cout << "Amb " << n << " terme(s) obtenim " << aproxima_e(n) << endl;
 }
}